Performance – Science4Performance

Relative Energy Deficit in Sport (RED-S)

EnergyBalance

Unfortunately an increasing proportion of the population of western society has fallen into the habit consuming far more calories than required, resulting an a huge increase in obesity, with all the associated negative health consequences. At the opposite end of the spectrum, a smaller but important group experiences problems stemming from insufficient energy intake. This group includes certain competitive athletes, especially those involved in sports or dance, where a low body weight confers a performance advantage. A new infographic draws attention to this problem and highlights the fact that the individuals have control over the factors that can put them on the path to optimal health and performance.

RED-S

The human body requires a certain amount of energy to perform normal metabolic functions, including, maintaining homeostasis, cardiac and brain activity. The daily requirement is around 2,000 kcal for women and 2,500 kcal for men. Additional energy intake is required to balance the energy requirements any physical activities performed.

Athletes and dancers need to eat more than sedentary people, but they can fall into an energy deficit in two ways.

Reducing energy intake, while maintaining the same training load. This is typically an intentional decision, in order to lose weight, in the belief that this might improve performance. It can also arise unintentionally, perhaps due to failing to calculate energy demands of the training programme.
Increasing training load, while maintaining the same energy intake. This can often occur unintentionally, as a result of a more intensive training session or a shift into a higher training phase. Some athletes or dancers perform extra training sessions while deliberately failing to eat more, in the hope, once again, that this might improve performance.

While most of the population would benefit from a period of moderate energy deficit. High level athletes and dancers tend to be very lean, to the extent that losing further weight compromises health and performance. The reason is that the endocrine system is forced to react to an energy deficit by scaling back or shutting down key metabolic systems. For example, levels of the sex hormones testosterone and oestrogen can fall, leading to, among other things, reductions in bone density. Unlike men, women have a warning sign, in the form of an interruption or cessation of menstruation. Both men and women with RED-S are likely to suffer from a failure to achieve their peak athletic performance.

Achieving peak performance

Fortunately athletes have control over the levers that lead to peak performance. These are nutrition, training load and, of course, recovery. Consistently fuelling for the energy required, whilst ensuring that the body has adequate time to recover, allows the endocrine system to trigger the genes that lead to the beneficial outcomes of exercise, such as improved cardiovascular efficiency, effective muscular development, optimal body composition, healthy bones and a fully functional immune system. These are the changes required to reach the highest levels of performance.

Screenshot 2019-04-08 at 12.19.45

Don’t ride your bike like an astronaut

Screenshot 2019-04-05 at 17.13.59

Astronauts return from the International Space Station with weak bones, due to the lack of gravitational forces. It is surprising to learn that competitive cyclists can experience similar losses in bone density over the period of a race season.

The problem is called Relative Energy Deficiency is Sport (RED-S). This occurs when lean athletes reach a tipping point where the benefits of losing weight become overwhelmed by negative impacts on health. When deprived of sufficient energy intake to match training load, certain metabolic systems become impaired or shut down.

Colleagues from Durham University and I recently published a study investigating what cyclists at risk of RED-S can do to improve their health and performance. It is freely available and written in an accessible way, without the requirement for specialist expertise.

Race performance

Race performance was measured by the number of British Cycling points accumulated over the season. This was correlated with power (FTP and FTP/kg) and training load. However, changes in energy availability proved to be an important factor. After adjusting for FTP, cyclists who improved their fuelling (green triangles) gained, on average, 95 points more than those who made no change. In contrast, those who restricted their nutrition (red crosses) accumulated 95 fewer points and reported fatigue, illness and injury.

Figure2 600 — Race Performance versus FTP and changes in Energy Availability (EA)

The nutritional advice included recommendations on adequate fuelling before, during and after rides. Also see my previous article on fuelling for the work required.

Bone health

Competitive road cyclists can fall into an energy deficit due to the long hours of training they complete. Although an initial loss of excess body weight can lead to performance improvements, athletes need to maintain a healthy body mass. The lumbar spine is particularly sensitive to deficiencies of energy availability.

In cyclists, the lower back also fails to benefit from the gravitational stresses of weight-bearing sports. This is why, in addition to nutritional advice, study participants were recommended some basic skeletal loading exercises (yes, that is me in the pictures).

The cyclists fell into three general groups: those who made positive changes to nutrition and skeletal loading, those who made negative changes and the remainder. The resulting changes in bone mineral density over a six month period were striking, with highly statistically significant differences observed between the groups.

Those making positive changes (green triangles) saw significant gains in bone mineral density, while those making negative changes (red crosses) saw equally significant negative losses in bone density. Any individual observation outside the band of the least significant change (LSC) is indicative of a material change in bone health.

Figure1 600 — Changes in Lumbar Bone Mineral Density versus Behaviour Changes

Conclusions

The study provided strong evidence of the benefits of positive changes and the costs of negative changes in nutrition and skeletal loading exercises. It was noted that certain cyclists found it hard to overcome psychological barriers preventing them from deviating from their current routines. It is hoped that such strong statistical results will help these vulnerable athletes make beneficial behavioural changes

References

Clinical evaluation of education relating to nutrition and skeletal loading in competitive male road cyclists at risk of relative energy deficiency in sports (RED-S): 6-month randomised controlled trial, Nicola Keay, Gavin Francis, Ian Entwistle, Karen Hind. BMJ Open Sport and Exercise Medicine Journal, Volume 5, Issue 1. http://dx.doi.org/10.1136/bmjsem-2019-000523

Fuel for the work required: periodisation of carbohydrate intake

screenshot2019-01-31at16.06.16 — Fuel for the work required, Impey et al, Sports Med (2018) 48:1031–1048

Last week I attended an event announcing the forthcoming launch of a new fitness app called Pillar. It offers combined training and nutrition advice to help athletes achieve their goals. Pillar is backed by a strong scientific team including Professor James Morton, Team Sky Head of Performance Nutrition, and Professor Graeme Close, England Rugby Head of Performance Nutrition.

James Morton gave a fascinating presentation about the periodisation of carbohydrate (CHO) fuelling, including a detailed description of the nutrition strategy he created to support Chris Froome’s famous 80km attack on stage 19 of the 2018 Giro d’Italia. His recent paper explains the underlying science. These are some of the key points.

Always go into competition fully fuelled with carbohydrate
- Well-fuelled athletes perform for longer at higher intensities than those with depleted reserves
- Basic biochemistry: fat burning is too slow and supplies of the phosphocreatine are too small to sustain intensities over 85% of VO2max
- Theory is backed up by experiment
There are pros and cons to training with low levels of carbohydrate
- Positive effects: Improved fat burning, changes in cell signalling, gene expression and enzyme/protein activity, potential to save precious glycogen stores for crucial attacks later in a race
- Negative effects: Inconsistent evidence of improved performance, ability to complete training session may be compromised, reduced immunity, risks to bone health, loss of top end for those on high fat/low carb (ketogenic) diet
Different ways to train with low carbohydrate
- doing two sessions in one day with minimal refuelling
- low carb evening meal and breakfast: sleep low, train low the next morning
- fasted rides
- high fat/low carb diet

Is there a structured method of training that provides the benefits without the negatives?

The authors propose a glycogen threshold hypothesis
- Positive effects seem to be dependent on commencing with muscle glycogen levels within a specific range
- Levels have to be low enough to promote positive effects
- But when too low, protein synthesis may be impaired and the ability to complete sessions is compromised
This leads to the idea of periodising carbohydrate consumption, meal by meal, around planned training sessions
“Fuelling for the work required”
- low carbs before and during lighter training sessions
- high carbs in preparation for and during rides with greater intensities
- always refuel after training
The diagram above provides an example for an elite endurance cyclist
- The red, amber, green colour coding indicates low, medium or high carbohydrate consumption
- On day 1, the athlete aims to “train high” for a hard session
- A lighter evening meal on day 1 prepares to “sleep low, train low” ahead of a lower intensity session on day 2
- Carbohydrate intake rises after exercise on day 2 in anticipation of a high intensity session on day 3
- Fuelling is moderated on the evening of day 3 as day 4 is assigned as a recovery day
- Carbohydrate rises later on day 4 to prepare for the next block of training
The Pillar app aims to provide these leading edge scientific principles to amateur cyclists and other athletes

In order to put this into action, you need to know how much carbohydrate you are consuming. My assumption has been that my diet is reasonably healthy, but I have never actually measured it. So I have been experimenting with free app MyFitnessPal that can be downloaded onto your phone. This provides a simple and convenient way to track the nutritional composition of your diet, including a barcode scanner that recognises most foods. You can link it to other apps such as Training Peaks to take account of energy expended. However, neither of these tools plans nutrition ahead of training sessions. Pillar aims to fill this gap. It will be interesting to see whether this turns out to be successful.

References

Fuel for the Work Required: A Theoretical Framework for Carbohydrate Periodization and the Glycogen Threshold Hypothesis, SG Impey, MA Hearris, KM Hammond, JD Bartlett, J Louis, G Close, JP Morton, Sports Med (2018) 48:1031–1048, https://doi.org/10.1007/s40279-018-0867-7

Fuel for the work required: a practical approach to amalgamating train-low paradigms for endurance athletes, Impey SG, Hammond KM, Shepherd SO, Sharples AP, Stewart C, Limb M, Smith K, Philp A, Jeromson S, Hamilton DL, Close GL, Morton JP, Physiol Rep. 2016 May;4(10). pii: e12803. doi: 10.14814/phy2.12803

Low carbohydrate, high fat diet impairs exercise economy and negates the performance benefit from intensified training in elite race walkers, Burke LM, Ross ML, Garvican-Lewis LA, Welvaert M, Heikura IA, Forbes SG, Mirtschin JG, Cato LE, Strobel N, Sharma AP, Hawley JA. J Physiol. 2017;595:2785–807

Low energy availability assessed by a sport-specific questionnaire and clinical interview indicative of bone health, endocrine profile and cycling performance in competitive male cyclists, BMJ Open Sport & Exercise Medicine,https://doi.org/10.1136/bmjsem-2018-000424

Machine learning for a medical study of cyclists

Screen Shot 2018-10-11 at 15.28.46

This blog provides a technical explanation of the analysis underlying the medical paper about male cyclists described previously. Part of the skill of a data scientist is to choose from the arsenal of machine learning techniques the tools that are appropriate for the problem at hand. In the study of male cyclists, I was asked to identify significant features of a medical data set. This article describes how the problem was tackled.

Data

Fifty road racing cyclists, riding at the equivalent of British Cycling 2nd category or above, were asked to complete a questionnaire, provide a blood sample and undergo a DXA scan – a low intensity X-ray used to measure bone density and body composition. I used Python to load and clean up the data, so that all the information could be represented in Pandas DataFrames. As expected this time-consuming, but essential step required careful attention and cross-checking, combined with the perseverance that is always necessary to be sure of working with a clean data set.

The questionnaire included numerical data and text relating to cycling performance, training, nutrition and medical history. As a result of interviewing each cyclist, a specialist sports endocrinologist identified a number of individuals who were at risk of low energy availability (EA), due to a mismatch between nutrition and training load.

Bone density was measured throughout the body, but the key site of interest was the lumbar spine (L1-L4). Since bone density varies with age and between males and females, it was logical to use the male, age-adjusted Z-score, expressing values in standard deviations above or below the comparable population mean.

The measured blood markers were provided in the relevant units, alongside the normal range. Since the normal range is defined to cover 95% of the population, I assumed that the population could be modelled by a gaussian distribution in order to convert each blood result into a Z-score. This aligned the scale of the blood results with the bone density measures.

Analysis

I decided to use the Orange machine learning and data visualisation toolkit for this project. It was straightforward to load the data set of 46 features for each of the 50 cyclists. The two target variables were lumbar spine Z-score (bone health) and 60 minute FTP watts per kilo (performance). The statistics confirmed the researchers’ suspicion that the lumbar spine bone density of the cyclists would be below average, partly due to the non-weight-bearing nature of the sport. Some of the readings were extremely low (verging on osteoporosis) and the question was why.

Given the relatively small size of the data set (a sample of 50), the most straightforward approach for identifying the key explanatory variables was to search for an optimal Decision Tree. Interestingly, low EA turned out to be the most important variable in explaining lumbar spine bone density, followed by prior participation in a weight-bearing sport and levels of vitamin D (which was, in most cases, below the ideal level of athletes). Since I had used all the data to generate the tree, I made use of Orange’s data sampler to confirm that these results were highly robust. This had some similarities with the Random Forest approach. Although Orange produces some simple graphical tools like the following, I use Python to generate my own versions for the final publication.

Decision Tree from Orange

Published Decision Tree

Finding a robust decision tree is one thing, but it was essential to verify whether the decision variables were statistically significant. For this, Orange provides box plots for discrete variables. For my own peace of mind, I recalculated all of the Student’s T-statistics to confirm that they were correct and significant. The charts below show an example of an Orange box plot and the final graphic used in the publication.

Orange Box Plot

Final Box Plots

The Orange toolkit includes other nice data visualisation tools. I particularly liked the flexibility available to make scatter plots. This inspired the third figure in the publication, which showed the most important variable explaining performance. This chart highlights a cluster of three cyclists with low EA, whose FTP watts/kg were lower than expected, based on their high training load. I independently checked the T-statistics of the regression coefficients to identify relationships that were significant, like training load, or insignificant, like percentage body fat.

Orange Scatter Plot

Published Scatter Plot

Conclusions

The Orange toolkit turned out to be extremely helpful in identifying relationships that fed directly into the conclusions of an important medical paper highlighting potential health risks and performance drivers for high level cyclists. Restricting nutrition through diet or fasted rides can lead to low energy availability, that can cause endocrine responses in the body that reduce lumbar spine bone density, resulting in vulnerability to fracture and slow recovery. This is know as Relative Energy Deficiency in Sport (RED-S). Despite the obsession of many cyclists to reduce body fat, the key variable explaining functional threshold power watts/kg was weekly training load.

References

Relative Energy Deficiency in Sport, British Association of Sports and Exercise Medicine

Synergistic interactions of steroid hormones, British Journal of Sports Medicine

Cyclists: Make No Bones About It, British Journal of Sports Medicine

Male Cyclists: bones, body composition, nutrition, performance, British Journal of Sports Medicine

Fuelling for Cycling Performance

Some commentators were skeptical of Team Sky’s explanation for Chris Froome’s 80km tour-winning attack on stage 19 of the Giro. His success was put down to the detailed planning of nutrition throughout the ride, with staff positioned at strategic refuelling points along the entire route. If you consider how skeletal the riders look after two and a half weeks of relentless competition, along with the limits on what can be physically absorbed between stages, the nutrition story makes a lot of sense. Did Yates, Pinot and Aru dramatically fall by the wayside simply because they ran out of energy?

The best performing cyclists have excellent balancing skills. This includes the ability to match energy intake with energy demand. The pros benefit from teams of support staff monitoring every aspect of their nutrition and performance. However, many serious club-level cyclists pick up fads and snippets of information from social media or the cycling press that lead them to try out all kinds ideas, in an unscientific manner, in the hope of achieving an improvement in performance. Some of these activities have potentially harmful effects on the body.

Competitive riders can become obsessed with losing weight and sticking to extremely tough training schedules, leading to both short-term and long-term energy deficits that are detrimental to both health and performance. One of the physiological consequences can be a reduction in bone density, which is particularly significant for cyclists, who do not benefit from gravitational stress on bones, due to the non-weight-bearing nature of the sport. In a recent paper, colleagues at Durham University and I describe an approach for identifying male cyclists at risk of Relative Energy Deficit in Sport (RED-S).

You need a certain amount of energy simply to maintain normal life processes, but an athlete can force the body into a deficit in two ways: by intentionally or unintentionally restricting energy intake below the level required to meet demand or by increasing training load without a corresponding increase in fuelling.

EnergyBalance

Our bodies have a range of ways to deal with an energy deficit. For the average, slightly overweight casual cyclist, burning some fat is not a bad thing. However, most competitive cyclists are already very lean, making the physiological consequences of an energy deficit more serious. Changes arise in the endocrine system that controls the body’s hormones. Certain processes can shut down, such as female menstruation, and males can experience a reduction in testosterone. Sex steroids are important for maintaining healthy bones. In our study of 50 male competitive cyclists, the average bone density in the lumbar spine, measured by DXA scan, was significantly below normal. Some relatively young cyclists had the bones of a 70 year old man!

The key variable associated with poor bone health was low energy availability, i.e. male cyclists exhibiting RED-S. These riders were identified using a questionnaire followed by an interview with a Sports Endocrinologist. The purpose of the interview was to go through the responses in more detail, as most people have a tendency to put a positive spin on their answers. There were two important warning signs.

Long-term energy deficit: a prolonged significant weight reduction to achieve “race weight”
Short-term energy deficit: one or more fasted rides per week

Among riders with low energy availability, bone density was not so bad for those who had previously engaged in a weight-bearing sport, such as running. For cyclists with adequate energy availability, those with vey low levels of vitamin D had weaker bones. Across the 50 cyclists, most had vitamin D levels below the level of 90 nmol/L recommended for athletes, including some who were taking vitamin D supplements, but clearly not enough. Studies have shown that the advantages of athletes taking vitamin D supplements include better bone health, improved immunity and stronger muscles, so why wouldn’t you?

In terms of performance, British Cycling race category was positively related with a rider’s power to weight ratio, evaluated by 60 minute FTP per kg (FTP60/kg). Out of all the measured variables, including questionnaire responses, blood tests, bone density and body composition, the strongest association with FTP60/kg was the number of weekly training hours. There was no significant relationship between percentage body fat and FTP60/kg. So if you want to improve performance, rather than starving yourself in the hope of losing body fat, you are better off getting on your bike and training with adequate fuelling.

Cyclists using power meters have the advantage of knowing exactly how many calories they have used on every ride. In addition to taking on fuel during the ride, especially when racing, the greatest benefits accrue from having a recovery drink and some food immediately after completing rides of more than one hour.

For those wishing to know more about RED-S, the British Association of Sports and Exercise Medicine has provided a web resource.

A related blog will explore the machine learning and statistical techniques used to analyse the data for this study.

References

Relative Energy Deficiency in Sport, British Association of Sports and Exercise Medicine

Synergistic interactions of steroid hormones, British Journal of Sports Medicine

Cyclists: Make No Bones About It, British Journal of Sports Medicine

Male Cyclists: bones, body composition, nutrition, performance, British Journal of Sports Medicine

Strava – Automatic Lap Detection

Screen Shot 2018-08-04 at 16.30.58 — Opening Laps of Hillingdon Race

As you upload your data, you accumulate a growing history of rides. It is helpful to find ways of classifying different types of activities. Races and training sessions often include laps that are repeated during the ride. Many GPS units can automatically record laps as you pass the point where you began your ride or last pressed the lap button. However, if the laps were not recorded on the device, it is tricky to recover them. This article investigates how to detect laps automatically.

First consider the simple example of a 24 lap race around the Hillingdon cycle circuit. Plotting the GPS longitude and latitude against time displays repeating patterns. It is even possible to see the “omega curve” in the longitude trace. So it should be possible to design an algorithm that uses this periodicity to calculate the number of laps.

Screen Shot 2018-08-03 at 19.07.16 This is a common problem in signal processing, where the Fourier Transform offers a neat solution. This effectively compares the signal against all possible frequencies and returns values with the best fit in the form of a power spectrum. In this case, the frequencies correspond to the number of laps completed during the race. In the bar chart below, the power spectrum for latitude shows a peak around 24. The high value at 25 probably shows up because I stopped my Garmin slightly after the finish line. A “harmonic” also shows up at 49 “half laps”. Focussing on the peak value, it is possible to reconstruct the signal using a frequency of 24, with all others filtered out.

Screen Shot 2018-08-03 at 19.20.38

So we’re done – we can use a Fourier Transform to count the laps! Well not quite. The problem is that races and training sessions do not necessarily start and end at exactly the starting point of a lap. As a second example, consider my regular Saturday morning club run, where I ride from home to the meeting point at the centre of Richmond Park, then complete four laps before returning home. As show in the chart below, a simple Fourier Transform approach suggests that ride covered 5 laps, because, by chance, the combined time for me to ride south to the park and north back home almost exactly matches the time to complete a lap of the park. Visually it is clear that the repeating pattern only holds for four laps.

Screen Shot 2018-08-03 at 19.35.07

Although it seems obvious where the repeating pattern begins and ends, the challenge is to improve the algorithm to find this automatically. A brute force method would compare every GPS location with every other location on the ride, which would involve about 17 million comparisons for this ride, then you would need to exclude the points closely before or after each recording, depending on the speed of the rider. Furthermore, the distance between two GPS points involves a complex formula called the haversine rule that accounts for the curvature of the Earth.

Fortunately, two tricks can make the calculation more tractable. Firstly, the peak in the power spectrum indicates roughly how far ahead of the current time point to look for a location potentially close to the current position. Given a generous margin of, say, 15% variation in lap times, this reduces the number of comparisons by a whole order of magnitude. Secondly, since we are looking for points that are very close together, we only need to multiply the longitudes by the cosine of the latitude (because lines of longitude meet at the poles) and then a simple Euclidian sum the squares of the differences locates points within a desired proximity of, say, 10 metres. This provides a quicker way to determine the points where the rider was “lapping”. These are shaded in yellow in the upper chart and shown in red on a long/latitude plot below. The orange line on the upper chart shows, on the right hand scale, the rolling lap time, i.e. the number of seconds to return to each point on the lap, from which the average speed can be derived.

Screen Shot 2018-08-03 at 20.26.18

Two further refinements were required to make the algorithm more robust. One might ask whether it makes a difference using latitude or longitude. If the lap involved riding back and forth along a road that runs due East-West, the laps would show up on longitude but not latitude. This can be solved by using a 2-dimensional Fourier Transform and checking both dimensions. This, in turn, leads to the second refinement, exemplified by the final example of doing 12 ascents of the Nightingale Lane climb. The longitude plot includes the ride out to the West, 12 reps and the Easterly ride back home.

Screen Shot 2018-08-03 at 20.34.02

The problem here was that the variation in longitude/latitude on the climb was tiny compared with the overall ride. Once again, the repeating section is obvious to the human eye, but more difficult to unpick from its relatively low peak in the power spectrum. A final trick was required: to consider the amplitude of each frequency in decreasing order of power and look out for any higher frequency peaks that appear early on the list. This successfully identified the relevant part of the ride, while avoiding spurious observations for rides that did not include laps.

The ability for an algorithm to tag rides if they include laps is helpful for classifying different types of sessions. Automatically marking the laps would allow riders and coaches to compare laps against each other over a training session or a race. A potential AI-powered robo-coach could say “Ah, I see you did 12 repeats in your session today… and apart from laps 9 and 10, you were getting progressively slower….”

Suddenly Summer in Richmond Park

Tour de Richmond Park Leaderboard – year to date 2018

Screen Shot 2018-04-20 at 14.54.42

This week’s dramatic change in the weather has seen a string of quick laps recorded for the Tour de Richmond Park. Twelve out of the fastest fifteen efforts were completed on 18/19 April. Apart from the sheer pleasure of finally being able to ride in short sleeves, two meteorological factors came into play: higher temperatures and a favourable wind direction.

As noted in an earlier blog, changes in temperature have a far greater impact on air density than variations in atmospheric pressure and humidity. When I completed a lap last week, the temperature was 6^oC, but on 19 April it was closer to 26^oC. The warmer weather had the effect of reducing air density by more than 7%. Theoretically, this should allow you to ride about 2% faster for the same effort. Using a physics model I built last year to analyse Strava segments, it is possible to estimate the effect of variations in the factors that determine your position on the leaderboard. Based on an average power of 300W and some reasonable estimates of other variables, this rise in temperature would reduce your time from 16:25 to 16:04 (as expected, 2% quicker).

The other key factor is the wind. On 18/19 April, it was blowing from the south or southeast. This was not the mythical easterly that provides a tailwind up Sawyers Hill, but according to the analysis in another earlier blog, it is generally beneficial for doing a quick lap around the park.

I clocked up a decent time this morning, to reach 15th place on the year-to-date leaderboard, but I failed to take my own advice on the best time of day. The traffic tends to be lighter first thing in the morning or in the evening, when the park closes. After waiting until mid-morning for the temperature to rise, I ended up being blocked by slow-moving vehicles on two occasions.

Although it was frustrating having to brake for traffic, the really puzzling thing was an average power reading of 254W. This is much lower than the other riders on the leaderboard. Last week, I did a lap in 16:44 at an average power of 313W, which seems much more reasonable. Admittedly, I was wearing a skin suit today, but that would not have saved 50W. It is possible that I had some drafting benefit from the numerous cars in the park and some favourable gusts of wind. However, my suspicion is that my Garmin Vector pedals had not calibrated correctly, after I switched them from my road bike, before today’s ride.

The concluding message is get on your bike and enjoy the sunshine. And why not try to beat your best time for the Tour de Richmond Park?

Cycling Data Science – building models

Screen Shot 2017-12-24 at 21.19.31.png In the previous blog, I explored the structure of a data set of summary statistics from over 800 rides recorded on my Garmin device. The K-means algorithm was an example of unsupervised learning that identified clusters of similar observations without using any identifying labels. The Orange software, used previously, makes it extremely easy to compare a number of simple models that map a ride’s statistics to its type: race, turbo trainer or just a training ride. Here we consider Decision Trees, Random Forests and Support Vector Machines.

Decision Trees

Perhaps the most basic approach is to build a Decision Tree. The algorithm finds an efficient way to make a series of binary splits of the data set, in order to arrive at a set of criteria that separates the classes, as illustrated below.

The first split separates the majority of training rides from races and turbo trainer sessions, based on an average speed of 35.8km/h. Then Average Power Variance helped identify races, as observed in the previous blog. After this, turbo trainer sessions seemed to have a high level of TISS Aerobicity, which relates to the percentage of effort done aerobically. Pedalling balance, fastest 500m and duration separated the remaining rides. An attractive way to display these decisions is to create a Pythagorean Tree, where the sides of each triangle relate to the number of observations split by each decision.

Screen Shot 2017-12-24 at 16.32.02 — Pythagorean Tree

Random Forests

Many alternative sets of decisions could separate the data, where any particular tree can be quite sensitive to specific observations. A Random Forest addresses this issue by creating a collection of different decision trees and choosing the class by majority vote. This is the Pythagorean Forest representation of 16 trees, each with six branches.

Support Vector Machines

A Support Vector Machine (SVM) is a widely used model for solving this kind of categorisation problem. The training algorithm finds an efficient way to slice the data, that largely separates the categories, while allowing for some overlap. The points that are closest to the slices are called support vectors. It is tricky to display the results in such a high dimensional space, but the following scatter plot displays Average Power Variance versus Average Speed, where the support vectors are shown as filled circles.

SVM — Support Vectors shown as filled circles

Comparison of results

A Confusion Matrix provides a convenient way to compare the accuracy of the models. This correlates the predictions versus the actual category labels. Out of the 809 rides, only 684 were labelled. The Decision Tree incorrectly labelled 20 races and 7 turbos as training rides. The Random Forest did the best job, with only six misclassifications, while the SVM made 11 errors.

Looking at the classification errors can be very informative. It turns out that the two training rides classified as races by the SVM had been accidentally mislabelled – they were in fact races! Furthermore, looking at the five races the that SVM classified as training rides, I punctured in one, I crashed in another and in a third race, I was dropped from the lead group, but eventually rolled in a long way behind with a grupetto. The Random Forest also found an alpine race where my Garmin battery failed and classified it as a training ride. So the misclassifications were largely understandable.

After correcting the data set for mislabelled rides, the Random Forest improved to just two errors and the SVM dropped to just eight errors. The Decision Tree deteriorated to 37 errors, though it did recognise that the climbing rate tends to be zero on a turbo training session.

Prediction

Having trained three models, we can take a look at the sample of 125 unlabelled rides. The following chart shows the predictions of the Random Forest model. It correctly identified one race and suggested several turbo trainer sessions. The SVM also found another race.

asapv — Random Forest predictions of unlabelled rides

Conclusions

Several lessons can be learned from these experiments. Firstly, it is very helpful to start with a clean data set. But if this is not the case, looking at the misclassified results of a decent model can be useful in catching mislabelled data. The SVM seemed to be good for this task, as it had more flexibility to fit the data than the Decision Tree, but it was less prone to overfit the data than the Random Forest.

The Decision Tree was helpful in quickly identifying average speed and power variance (chart below) as the two key variables. The SVM and Random Forest were both pretty good, but less transparent. One might improve on the results by combining these two models.

apv — Distribution of APV (large peak at zero is where no power was recorded for ride)

The next blog will explore this topic further.

Cycling Data Science – clusters

Screen Shot 2017-12-11 at 13.38.30

Data Science is a hot topic that is impacting a range of diverse areas from business to sport. With so many cyclists collecting and uploading their data, there is plenty of raw material from which to draw interesting insights. This is the first in a series of articles exploring applications of data science in the field of cycling, beginning with the concept of clustering.

As a data set, I took all my Garmin files covering 2014-2017. Having previously uploaded them onto Golden Cheetah (GC), I took advantage of the API that allows external programmes, such as Python, to retrieve data. I also used a Python library to download the same rides from Strava, where I had recorded additional information about the rides.

After a certain amount of (rather time-consuming) tidying up, I ended up with over 800 rides. Each ride had over 200 summary statistics calculated by GC, as well as other meta-data, such as whether the ride was a race or turbo session. The metrics included all the standard items, such as time, distance, speed, heart rate, power, elevation gain, TSS, normalised power, as well as more esoteric metrics like “Time expended when Power is above CP and W’ bal is between 50% and 75% of W'”. When each ride is represented by a point in 200-dimensional space, it is easy to be overwhelmed. As a coach or an informed rider, which metrics are the most meaningful? This is precisely where data science steps in.

I decided to use some open source machine learning and data visualisation software called Orange. This makes it very straightforward to set up simple pipelines using a toolbox of standard approaches, as illustrated above.

One of the first things to do was to ask the computer to look for clusters of rides with similar characteristics. Orange has a useful feature that finds informative projections of the data that can be displayed on a scatter plot. As a first cut, the K-means algorithm categorised the data into four clusters that were largely explained by the time of day and the duration of the ride.

Screen Shot 2017-12-11 at 16.34.22 — Duration of ride (in seconds) versus Time of day (seconds since midnight)

Although this makes a pretty graph, it simply tells us that I start a lot of rides in the morning, but do quite a few in the afternoon and evening. The green cluster includes my longer rides that rather obviously have to start earlier in the day. The scale is annoyingly shown in seconds, so a duration of 1800 would be a five hour ride. The blue band runs from about 1:30pm to about 6:30pm.

Grouping rides by time of day was not very helpful, so I filtered out that variable and searched again for rides that were similar in terms of effort. This made the results much more interesting. Distance and Average Power Variance (APV) were among the most informative metrics. The following scatter plot does a very good job of separating out races (shown in green), from normal rides and turbo trainer sessions (red). The points I did not have time to label are shown in grey.

Average Power Variance measures the mean power deviation with respect to its 30 second moving average. This will be high when power output is continually changing sharply, as it does on very short town centre courses or the Crystal Palace loop, where you are repeatedly sprinting out of corners. When racing on the Hillingdon and Dunsfold circuits or longer Surrey League routes, power is still much more variable than on a club ride. The band of Saturday club riders is very obvious at 53km: four laps of Richmond Park, with varying levels of APV depending on how aggressively the group was riding. You can also see that I quite often do only one or two laps, at about 19km and 30km. Short TTs and hill climb races tend to have less power variability. This was also the case on the endlessly long climbs encountered on the Haute Route. Lastly, turbo sessions have much lower APV because, even if target power levels vary, they tend to be sustained at the same level for each segment.

It is worth noting that APV is not correlated with the Variability Index, which is the ratio of normalised power to average power. APV is affected by continual changes in power output, whereas the Variability Index is strongly affected by power peaks, even if they a relatively few. The two power files below illustrate the difference.

Screen Shot 2017-12-11 at 17.39.55 — Crit race: High APV Low VI

Screen Shot 2017-12-11 at 17.39.02 — Three sprints: Low APV High VI

Conclusions

This analysis draws attention to Average Power Variance as a useful metric that is high for circuit and road races, but lower for TTs and long hilly races. The key observation for me is that relatively little of my training has a high APV.

The next part in this series zooms in on the races, to identify metrics associated with good and bad results.

Kings and Queens of the Mountains

Screen Shot 2017-11-09 at 18.40.09.png

I guess that most male cyclists don’t pay much attention to the women’s leaderboards on Strava. And if they do it might just be to make some puerile remark about boys being better than girls. From a scientific perspective the comparison of male and female times leads to some interesting analysis.

Assuming both men and women have read my previous blogs on choosing the best time, weather conditions and wind directions for the segment that suits their particular strengths, we come back to basic physics.

KOM or QOM time = Work done / Power = (Work against gravity + Drag x Distance + Rolling resistance x Distance) / (Mass x Watt/kg)

Of the three components of work done, rolling resistance tends to be relatively insignificant. On a very steep hill, most of the work is done against gravity, whereas on a flat course, aerodynamic drag dominates.

The two key factors that vary between men and women are mass and power to weight ratio (watts per kilo). A survey published by the ONS in 2010, rather shockingly reported that the average British man weighed 83.6kg, with women coming in at 70.2kg. This gives a male/female ratio of 1.19. KOM/QOM cyclists would tend to be lighter than this, but if we take 72kg and 60kg, the ratio is still 1.20.

Males generate more watts per kilogram due to having a higher proportion of lean muscle mass. Although power depends on many factors, including lungs, heart and efficiency of circulation, we can estimate the relative power to weight ratio by comparing the typical body composition of males and females. Feeding the ONS statistics into the Boer formula gives a lean body mass of 74% for men and 65% for women, resulting in a ratio of 1.13. This can be compared against the the useful table on Training Peaks showing maximal power output in Watts/kg, for men and women, over different time periods and a range of athletic abilities. The table is based on the rows showing world record performances and average untrained efforts. For world champion five minute efforts and functional threshold powers, the ratios are consistent with the lean mass ratio. It makes sense that the ratio should be higher for shorter efforts, where the male champions are likely to be highly muscular. Apparently the relative performance is precisely 1.21 for all durations in untrained people.

Screen Shot 2017-11-08 at 10.23.33

On a steep climb, where the work done against gravity dominates, the benefit of additional male muscle mass is cancelled by the fact that this mass must be lifted, so the difference in time between the KOM and the QOM is primarily due to relative power to weight ratio. However, being smaller, women suffer from the disadvantage that the inert mass of bike represents a larger proportion of the total mass that must be raised against gravity. This effect increases with gradient. Accounting for a time difference of up to 16% on the steepest of hills.

In contrast, on a flat segment, it comes down to raw power output, so men benefit from advantages in both mass and power to weight ratio. But power relates to the cube of the velocity, so the elapsed time scales inversely with the cube root of power. Furthermore, with smaller frames, women present a lower frontal area, providing a small additional advantage. So men can be expected to have a smaller time advantage of around 9%. In theory the advantage should continue to narrow as the gradient shifts downhill.

Theory versus practice

Strava publishes the KOM and QOM leaderboards for all segments, so it was relatively straightforward to check the basic model against a random selection of 1,000 segments across the UK. All leaderboards included at least 1,666 riders, with an overall average of 637 women and 5,030 men. One of the problems with the leaderboards is that they can be contaminated by spurious data, including unrealistic speeds or times set by groups riding together. To combat this, the average was taken of the top five times set on different dates, rather than simply to top KOM or QOM time.

The average segment length was just under 2km, up a gradient of 3%. The following chart plots the ratio of the QOM time to the KOM time versus gradient compared with the model described above. The red line is based on the lean body mass/world record holders estimate of 1.13, whereas the average QOM/KOM ratio was 1.32. Although there is a perceivable upward slope in the data for positive gradients, clearly this does not fit the data.

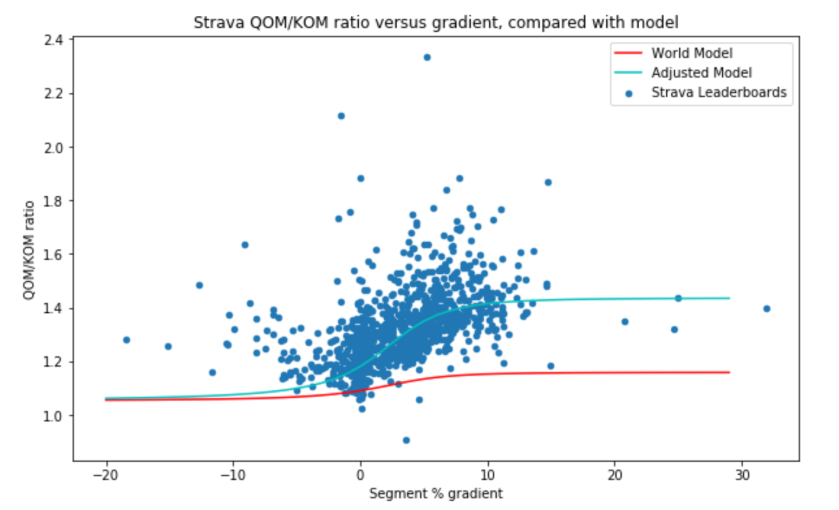
Screen Shot 2017-11-09 at 17.54.43

Firstly, the points on the left hand side indicate that men go downhill much more fearlessly than women, suggesting a psychological explanation for the observations deviating from the model. To make the model fit better for positive gradients, there is no obvious reason to expect the weight ratio of male to female Strava riders to deviate from the general population, so this leaves only the relative power to weight ratio. According to the model the QOM/KOM ratio should level off to the power to weight ratio for steep gradients. This seems to occur for a value of around 1.40, which is much higher than the previous estimates of 1.13 or the 1.21 for untrained people. How can we explain this?

A notable feature of the data set was that sample of 1,000 Strava segments was completed by nearly eight times as many men as women. This, in turn reflects the facts that there are more male than female cyclists in the UK and that men are more likely to upload, analyse, publicise and gloat over their performances than women.

Having more men than women, inevitably means that the sample includes more high level male cyclists than equivalent female cyclists. So we are not comparing like with like. Referring back to the Training Peaks table of expected power to weight ratios, a figure of 1.40 suggests we are comparing women of a certain level against men of a higher category, for example, “very good” women against “excellent” men.

A further consequence of having far more men than women is that is much more likely that the fastest times were recorded in the ideal conditions described in my previous blogs listed earlier.

Conclusions

There is room for more women to enjoy cycling and this will push up the standard of performance of the average amateur rider. This would enhance the sport in the same way that the industry has benefited as more women have joined the workforce.