Science4Performance – Science4Performance

Human Blood Protein Atlas

A recent report in Science announced the publication of a new human blood protein atlas, describing the disease signatures of thousands of proteins circulating in the blood. Minimally invasive protein profiling marks a step forward in the personalisation of medicine. Some interesting statistical and machine learning techniques were employed.

Blood Protein Study

The researchers’ methods included a technique called proximity extension assay (PEA), which makes use of highly specific probes of DNA strands to detect minute concentrations of proteins in the blood plasma. Amplification with PCR (Polymerase Chain Reactions) allowed 5,416 proteins to be evaluated.

A longitudinal dataset showed dramatic changes as children passed through adolescence to adulthood. The central part of the study was a cross-sectional analysis, where age, sex and BMI were identified as important explanatory factors. The signatures of 59 clinically relevant diseases, in seven classes, can be viewed interactively in The Human Protein Atlas.

Into the secretome

Rather than the hideaway of a reclusive cockney, the secretome refers to the ensemble of secreted proteins. From a data science perspective, the challenge was how to find the signatures of a wide range of diseases, based on the differential abundance of over 5,400 proteins. This was complicated by the fact that many proteins elevated by a particular disease were also found to be elevated in other diseases.

“To investigate the distinct and shared proteomics signatures across diseases, we performed differential abundance analyses. Several groups were used as controls, including healthy samples, a disease background consisting of all other diseases, and samples from the same disease class.”

The differential abundance of proteins was evaluated using normalised protein expression units (NPX). The volcano chart above plots the p-values against the multiplicative (fold) change in NPX, both on log scales. The red values on the right were unusually high and the blue values on the left was exceptionally low.

The researchers used a logistic LASSO approach to identify the importance of proteins in providing a signature of each disease against its cohort. In the case of HIV above, CRTAM was the most significant explanatory factor, even though CD6 had the most extreme p-value.

How does logistic LASSO work?

A logistic model is trained on target values of one or zero, in this case representing the presence or absence of a disease. Least absolute shrinkage and selection operator (LASSO) is a version of linear regression that selects the most relevant explanatory variables using L1 regularisation. Adding the sum of the absolute values of the regression coefficients to the objective function forces the contribution of irrelevant variables towards zero as the hyper-parameter, λ, is increased. This property was particularly useful for the disease signature problem, where there were thousands of potential explanatory proteins.

The tricky aspect of LASSO is tuning the hyper-parameter, λ. You want it to be high enough to eliminate irrelevant variables, but not so high that it discounts the useful explanatory features. In the protein study, this was addressed using cross-validation: randomly splitting the data into 70:30 training and test sets, then rerunning the regression for a range of λ values. The quality of a model can be assessed in terms of both its accuracy and its required number of inputs, using criteria such as the Akaike information criterion or Bayesian information criterion, which favour parsimony. Repeating the randomisation 100 times, the researchers could home in on an optimal value of λ. The regression coefficients of the resulting model could then be used to rank the importance of the relevant proteins, as shown in the right hand side of the panel above.

Personalised health

The potential for a cheap, annual blood test to screen the whole population is immense. Proteomics adds to the arsenal of resources available to help people stay healthy. Early indications of diseases like cancer can be critical in initiating treatment. There is plenty of room to broaden the scope beyond the current 59 diseases, to include rarer conditions, such as Motor Neurone Disease, which has impacted some top sportsmen. It would be extremely helpful to find proteins related to the apparent epidemic of mental health issues, which are hard to define and lack objective, quantitative diagnostic criteria.

Round Britain By Bike

This morning I cheered on Bernard Bunting as he embarked on an epic tour Round Britain By Bike to raise money for the Rare Dementia Support Centre.

Bernard has set himself the impressive target of riding around the coastline of Britain. He will start and end at Putney Bridge in London, visiting 50 checkpoints along the way. This involves some serious route planning. The problem reminded me of the famous Travelling Salesmen Problem, where the challenge is to find the shortest route that visits each of a list of cities and returns to the starting point.

Travelling Salesman Problem

Apart from cycling around Britain, the Travelling Salesman Problem is relevant in to circumstances, such as scheduling the order of supermarket deliveries or planning logistics for manufacturing processes. The problem is considered to be NP-hard, meaning that the number of combinations explodes exponentially as the number of cities increases. For example, considering only the order in which he passes the checkpoints, Bernard could set off for any of 49 destinations, then choose to go to any of 48 places, then one of the remaining 47 … before eventually returning to Putney Bridge, resulting in 49! (approximately 6.1 x 10⁶²) possible routes. This makes it very hard to be absolutely sure that any particular route is the shortest. For most problems the best you can do is come up with a fairly good route.

Elastic band – a greedy approach

I have always imagined a quick way to find a reasonably good approach is to visualise the cities marked with pins on a map. You start by putting an elastic band around the outside (a convex hull). Then you consider all the points inside the band and pull the elastic in around the closest point. Repeat until you have all the points. This is approach is “greedy” in the sense that it only looks one step ahead when choosing the best option. It starts slowly, but gets faster as the number of remaining points is reduced.

Greedy elastic band algorithm for a route around Britain

Tweaking it

One problem with the simple greedy approach is that it sometime produces a path that crosses itself. This is inefficient because it is alway an uncrossed path as always shorter. Although it is very easy to spot a crossed path, writing an algorithm that makes sure no path crosses any other is quite time-consuming. A simpler approach is to step around the current route and reuse the original trick of finding the closest point to each edge. If it is better to divert to that point, update the route. Repeat until no improvements are found. Tweaking the route around Britain slightly reduced the overall length.

This is the tweaking process running on a more complicated problem involving 300 checkpoints. Once the initial route is built, the tweaking process reduces the path length from 15.01 to 14.44. Python code can be found on GitHub in my TSP repository.

Getting real

Although tweaking the result shortened the route around the 50 British checkpoints, it does not follow the coastline and it jumps directly from St Ives to Johnston in Wales. So this solution is not particularly useful for Bernard’s planning. Practical route finding must take account of roads and physical barriers.

Fortunately Bernard will be following his GPS route on his bike computer. He also has a printed card for each day. Let’s hope he doesn’t get lost.

You can follow Bernard on Strava and news will be posted on his website. Please consider supporting Bernard by making a donation.

PEAQ Performance

If you are a cyclist, athlete, dancer or exerciser struggling to reach your full potential, your might have a mismatch between your training and what you are eating. Persistently running an energy deficit can have an adverse impact on your health and performance, sometimes leading to a condition called Relative Energy Deficiency in Sport (REDs). Optimal training adaptations and peak achievements rely on consistently fuelling for the work required.

I have created an app that generates a score based on a short Personal Energy Availability Questionnaire (PEAQ) designed to identify people at risk.

Personal Energy Availability Questionnaire (PEAQ)

The PEAQ is based on research published in BMJ Open Sport & Exercise Medicine, exploring the relationship between a REDs score derived from the questionnaire and quantified clinical consequences of low energy availability. A similar approach has been used in other research.

The app automates the scoring process and generates a free downloadable report that includes graphics and an interpretation of your result. It takes a few minutes to fill in your answers and the process is anonymous.

The report breaks down the overall score into three health categories. Physical health is based on body mass index (BMI) and injuries. Physiological factors include hormones, sleep and nutrition. Psychological wellbeing relates to habits and anxiety.

Relative energy deficiency

REDs is not confined to top athletes. It can occur in men and women of any age, at all levels of performance, across a spectrum of activities, including sports, exercise and dance.

Relative energy deficits can result from deliberate under-fuelling, particularly in activities where low body weight confers an aesthetic or performance advantage (dance, cycling, climbing, running etc.). Relative energy deficits can also arise, sometimes unintentionally, as a result of stepping up one’s training load without a corresponding increase in energy intake.

Health and performance risks

For evolutionary reasons, your body prioritises movement in the allocation of its energy budget. Energy availability is a measure of the amount of energy left over for day-to-day physiological processes: breathing, digestion, repair, brain function etc.. In an energy deficit, your body switches off inessential processes, such as reproduction. Poor bone health is one of the consequences of a reduction in sex steroid hormones. Other effects of low energy availability include fatigue, disrupted sleep and digestive problems.

For active people, low energy availability reduces your ability to perform high quality training/exercise and depletes your body’s ability to deliver the desired positive adaptations, such as muscle strength and endurance capacity.

Take a PEAQ

Please take advantage of the PEAQ. If you have worries or concerns about your results, Dr Nicky Keay offers personalised health advisory appointments. You can find valuable resources at BASEM.

Technical points

I built this educational health app in Python. It is hosted on the Streamlit Community Cloud. The code is on my GitHub page.

References

Mountjoy M, Ackerman KE, Bailey DM et al 2023 International Olympic Committee’s (IOC) consensus statement on Relative Energy Deficiency in Sport (REDs) British Journal of Sports Medicine 2023;57:1073-1098
Keay N Hormones, Health and Human Potential: A guide to understanding your hormones to optimise your health and performance, Sequoia books 2022
Keay N, Francis G, AusDancersOverseas Indicators and correlates of low energy availability in male and female dancers. BMJ Open in Sports and Exercise Medicine 2020
Nicolas J, Grafenuer S. Investigating pre-professional dancer health status and preventative health knowledge Front. Nutr. Sec. Sport and Exercise Nutrition. 2023 (10)
Keay N, Francis G. Longitudinal investigation of the range of adaptive responses of the female hormone network in pre- professional dancers in training March 2025 ResearchGate DOI: 10.13140/RG.2.2.30046.34880
Keay N. Current views on relative energy deficiency in sport (REDs). Focus Issue 6: Eating disorders. Cutting Edge Psychiatry in Practice CEPiP. 2024.1.98-102
Assessment of Relative Energy Deficiency in Sport, Malnutrition Prevalence in Female Endurance Runners by Energy Availability Questionnaire, Bioelectrical Impedance Analysis and Relationship with Ovulation status. Clinical Nutrition Open Science 2025S.
Sharp S, Keay N, Slee A. Body composition, malnutrition, and ovulation status as RED-S risk assessors in female endurance athletes, Clinical Nutrition ESPEN 2023, 58 :720-721
Keay N, Craghill E, Francis G Female Football Specific Energy Availability Questionnaire and Menstrual Cycle Hormone Monitoring. Sports Injr Med 2022; 6: 177
Nicola Keay, Martin Lanfear, Gavin Francis. Clinical application of monitoring indicators of female dancer health, including application of artificial intelligence in female hormone networks. Internal Journal of Sports Medicine and Rehabilitation, 2022; 5:24.
Nicola Keay, Martin Lanfear, Gavin Francis. Clinical application of interactive monitoring of indicators of health in professional dancers J Forensic Biomech, 2022, 12 (5) No:1000380
Keay, Francis, Hind Low energy availability assessed by a sport-specific questionnaire and clinical interview indicative of bone health, endocrine profile and cycling performance in competitive male cyclists BMJ Open Sports and Exercise Medicine 2018
Keay, Francis, Hind Clinical evaluation of education relating to nutrition and skeletal loading in competitive male road cyclists at risk of relative energy deficiency in sports (RED-S): 6-month randomised controlled trial BMJ Open Sports and Exercise Medicine 2019
Keay, Francis, Hind Bone health risk assessment in a clinical setting: an evaluation of a new screening tool for active populations MOJSports Medicine 2022;5(3):84-88. doi: 10.15406/mojsm.2022.05.00125″

Large Language Models for Cycling

Amid the fanfare about the extraordinary AI capabilities of large language models (LLMs), the race is on to produce LLM applications that actually do something useful. Several hurdles obstruct the way forward, including confabulation, privacy and limitations of training data. This article explains how Retrieval-Augmented Generation can address some of these issues and help find out some useful information about cycling.

Confabulation

Since they are trained only to predict the next word in a sentence, LLMs have no understanding of the text they generate. They can have a tendency to intersperse facts with inaccurate or untrue statements in a manner that seems entirely plausible and convincing. You should not rely on an LLM for advice on important decisions without validating its response. Note that if you ask an LLM for its sources, the citations may be imaginary or if they exist the references may not support the assertions.

One way to reduce the risk of confabulation is to ask the LLM to base its answer selected relevant documents.

Privacy

If you use an online ChatBot, everything you type or upload is stored on the provider’s server. This can be used as further training data or for snooping on users. There is a significant risk that a lot of personal and proprietary company information has already been hoovered up in this way. Companies need ways to sandbox internally developed LLM tools that contain sensitive data and prevent leakage of confidential information.

Privacy can be addressed by running LLMs on local networks. This is possible because inference is a simple task relative to training, which requires banks of data servers. Many free open-source models are available. Running an open-source model locally also avoids paying a subscription to an online provider.

Limitations of training data

LLMs are trained on vast generic data sets. This is a very expensive task, so they are typically frozen at some point in time. If you ask an LLM about current news events, it will typically tell you that it was trained on data up to a certain date in the past and has no knowledge of the event. The models may also lack specialised data in narrow domains.

RAG provides a way to supplement the original training set with selected additional information relevant to the field of interest.

RAG

Retrieval-Augmented Generation is an approach that provides an LLM with additional information to help it answer a query. For example, when asked about current affairs, it would be very helpful to retrieve a copy of today’s newspaper. Companies may wish to develop LLM-based applications with specialist knowledge of internal documentation. RAG makes this possible.

When you interact with an LLM, your conversation is presented to the model in the form of a huge string of numbers called an embedding. LLMs are trained so that sentences with similar words and meanings have similar embeddings. The idea of RAG is to take one or more relevant supplementary documents, split them up into chunks and store the embeddings of these chunks in a vector database. When a user presents a query, the database retrieves the embeddings of chunks that most closely match the query. In this way, the query can be augmented with relevant chunks of text from the source material. Note that this avoids the need to do additional expensive training or fine-tuning of the LLM on specialist topics.

One weakness of RAG is that most LLMs have not been trained specifically on the types of prompts used in RAG, though some companies, like Cohere, are working on this.

Cycling Through the Pandemic

I decided to try this out using a freely available book called Cycling Through the Pandemic, which has the slightly cryptic subtitle, Tactical Urbanism and the Implementation of Pop-Up Bike Lanes in the Time of COVID-19. This 250-page book was published in 2024, so it could not have been part of the training set for the LLM that I was using.

It is unbelievably easy to download and then run an open-source LLM on your local machine. All you need to do is download LM Studio. I decided to use an open-source LLM model called Meta-Llama-3.1-8B-Instruct-GGUF. I dragged and dropped the pdf of the book into the chat-box and started asking questions.

A transcript of my conversation is recorded below. At each step, LM Studio retrieved three chunks of text from the book it considered most relevant to the query, allowing me to check the reliability of the model’s interpretation.

The model answered in good English, basing its responses on the content of the book. It corrected itself when challenged on the claim that Bogotá is in France. It even responded in French to a question posed in French. In my view, RAG can be used to produce genuinely useful applications for LLMs.

RAG dialogue based on a book about the impact of COVID 19 on cycling

You
CyclingCOVID.pdf

What is tactical urbanism

Assistant
Meta-Llama-3.1-8B-Instruct-GGUF
Intermediate steps hidden. Click to expand.

Based on the provided information, tactical urbanism refers to a type of urban planning that involves temporary and low-cost interventions aimed at introducing rapid changes to urban spaces with a broader purpose in mind (Lydon and Garcia 2015). It can be seen as a practical approach to urban change where many small actions implemented at the hyper-local level can achieve longer-term goals of creating a liveable, walkable, sustainable community.

Tactical urbanism often involves shortcuts or rapid and unbureaucratic actions taken by municipalities in response to crises (Citation 1). It can be associated with grassroots initiatives but can also be used by authorities. This approach has been implemented in various contexts, including during the COVID-19 pandemic.

Tactical urbanism is characterized by its focus on temporary and flexible material approaches to urban change, which can be both a practical tool for citizens and enterprising governments alike (Citation 3).

It’s worth noting that there are different perspectives on tactical urbanism, with some viewing it as a means of achieving substantive change without state action, while others see the increasing professionalization of these activities as borrowing their material design language (Citation 2).

You
Why was cycling boosted by COVID 19?

Assistant
Meta-Llama-3.1-8B-Instruct-GGUF
Retrieved 3 relevant citations for user query
Done predicting
Cycling saw a boost during the COVID-19 pandemic for several reasons (Citation 2). Firstly, people had less need to travel due to home working and distance learning. Secondly, the fear of infection led to a strong decline in ridership on public transport, which benefited cycling. Additionally, active mobilities such as cycling were promoted as a means of staying fit and getting exercise when other recreational facilities were closed.

The pandemic also led to an increase in cycling for leisure activities (Buehler and Pucher 2021b), with the strongest increase seen on weekends and in the afternoon. This shift towards cycling as a leisure activity is likely due to the rise of “undirected travel,” or trips without a specific destination, which was encouraged by social distancing measures.

In France, for instance, the first COVID-19 related lockdown led to a rapid increase in cycling use (Buehler and Pucher 2022) and implemented temporary cycle paths. Governments saw cycling as a solution to develop health-friendly mobility while responding to the possible desertion of public transport due to fear of catching the virus (Citation 3).

You
Has the COVID related boost in cycling persisted

Assistant
Meta-Llama-3.1-8B-Instruct-GGUF
Retrieved 3 relevant citations for user query
Done predicting
The survey conducted in Geneva and Lausanne (Rérat et al. 2022; Schmassman and Rérat 2022) found that the COVID-related boost in cycling has largely persisted. The majority of respondents reported cycling as much or more often than before the pandemic, with a significant number even starting to cycle for the first time.

In Geneva, 42% of respondents cycled as much as before, while 44% cycled more often. In Lausanne, 58% cycled as much as before, and 27% cycled more often. This suggests that many people have adopted cycling as a mode of transport during the pandemic and are likely to continue using it.

The fact that 81% of respondents in Geneva (73% in Lausanne) agree or strongly agree that COVID cycle lanes make them feel safer also suggests that these temporary infrastructure projects had a lasting impact on cyclist safety and behavior.

However, as mentioned by Citation 2, the long-term sustainability of this boost is still uncertain. The study notes that most cycling infrastructure implemented during the pandemic involved existing projects, and it remains to be seen whether this “leap forward” will make a lasting difference in the trajectory of local public action or simply represent a spike on an upward graph.

Overall, while there are indications that the COVID-related boost in cycling has largely persisted, further analysis is needed to determine its long-term impact.

You
What has been the impact specifically in London?

Assistant
Meta-Llama-3.1-8B-Instruct-GGUF
Retrieved 3 relevant citations for user query
Done predicting
The impact of temporary cycling infrastructure and “Tactical Urbanist” approaches in London is a complex issue with both positive and negative effects.

Positive impacts include:

The introduction of School Streets, which have shown to promote mode shift towards active modes of travel (Hopkinson et al. 2021) and improve air quality at schools (Air Quality Consultants 2021).
The implementation of temporary cycle lanes and other small-scale projects aimed at improving the smaller residential or local streets in London.
These efforts are part of the Healthy Streets approach, which aims to promote a more sustainable transportation system in London.
However, there have also been negative impacts, including:

Variable outcomes between sites, with some schemes showing little effect (Citation 2).
Criticisms that some projects were implemented too quickly or without adequate consultation, leading to concerns about the speed and process of decision-making.
Vandalism of planters, bollards, and cameras used to prevent through-traffic in some areas (Citation 3).
Removal of Low Traffic Neighbourhoods, especially in Outer London, due to opposition from local residents.
The Temporary City report by Asa Thomas highlights the importance of balancing big change with small impact, emphasizing the need for careful planning and consultation when implementing new transportation projects.

You
What research was done in French cities?

Assistant
Meta-Llama-3.1-8B-Instruct-GGUF
Retrieved 3 relevant citations for user query
Done predicting
The research on French cities during the COVID-19 pandemic focused on understanding how urban planners and policymakers implemented measures to promote cycling and improve public transportation.

A study examined five French cities: Grenoble, Lyon, Montpellier, Rennes, and Bogotá (Citation 1). The study found that these cities had varying levels of population size, density, and surface area. For example, Bogotá was the most populous city with over 7 million inhabitants, while Grenoble had a smaller population of around 160,000.

Another study looked at the implementation of measures in French cities during the pandemic (Citation 2). The research found that some cities focused on improving cycling infrastructure within the city center, such as Lyon and Rennes. In contrast, other cities prioritized links between periurban municipalities or outer suburbs.

A book titled “Changing Bikeability: Everyday Cycling in Developed Territories” explores changing bikeability in French cities during the pandemic (Citation 3). The book examines six French cities: Grenoble, Lyon, Montpellier, Paris, Rennes, and Saint-Étienne. The research found that each city had its unique characteristics and ways of implementing measures to promote cycling.

These studies provide insights into how different types of cities implemented measures to improve cycling infrastructure during the pandemic, and whether these measures were made permanent.

You
Is Bogotá in France?

Assistant
Meta-Llama-3.1-8B-Instruct-GGUF
Retrieved 3 relevant citations for user query
Done predicting
No, Bogotá is not in France. According to Citation 1 and Citation 2, Bogotá is located in Colombia, and it has been compared with four French cities: Grenoble, Lyon, Montpellier, and Rennes.

In fact, the study mentioned in Citation 3 compares the cycling infrastructure in these four French cities (Grenoble, Lyon, Montpellier, and Rennes) with that of Bogotá, a city located in Colombia.

You
Quels ont été les résultats à Grenoble ?

Assistant
Meta-Llama-3.1-8B-Instruct-GGUF
Retrieved 1 relevant citations for user query
Done predicting
Les résultats obtenus à Grenoble sont mentionnés dans la citation :

“Nous avons contacté le Syndicat Mixte des Mobilités de l’Aire Grenobloise et réussi à obtenir la base de données du réseau cyclable. De plus, un stagiaire a effectué une interview avec un technicien de cette organisation, et sur plusieurs occasions, il est allé visiter le site pour voir si les voies temporaires (pop-up tracks) existaient toujours.”

Cela indique que les auteurs ont réussi à collecter des données sur le réseau cyclable de Grenoble en contactant la Syndicat Mixte des Mobilités de l’Aire Grenobloise et en effectuant une interview avec un technicien. Cependant, il n’y a pas d’information sur les résultats concrets de ces efforts.

Cependant, on peut trouver plus d’informations dans le graphique (Figure 8.2) qui montre différents types de voies temporaires installés dans les cinq villes étudiées, dont Grenoble.

39.77 tok/sec

•

234 tokens

•

3.34s to first token

•

Stop: eosFound

Cyclo-Social Networks

When Mexico’s Isaac del Toro and the Brit, Finlay Pickering, joined World Tour teams in 2024, they became part of an elite group. The structure of the professional cycling community differs from other types of social network, because the sport is organised around close-knit teams. You may have heard of the idea that everyone in the world is connected by six degrees of separation. Many social networks include key individuals who act as hubs linking disparate groups. How closely connected are professional cyclist? Which cyclists are the most connected?

Forming a link

An obvious way for cyclists to become acquainted is by being part of the same team. They spend long periods travelling, training, eating and relaxing together, often sharing rooms. Working as a team through the trials and tribulations of elite competition develops high degrees of camaraderie.

Each rider’s page on ProCyclingStats includes a team history. So I checked the past affiliations of all the current UCI world team riders. The idea was to build a graph where each node represented a rider, with edges connecting riders who had been in the same team. Each edge was weighted by the number of years a pair of riders had been in the same team, reflecting the strength of their relationship.

Cyclo-social network

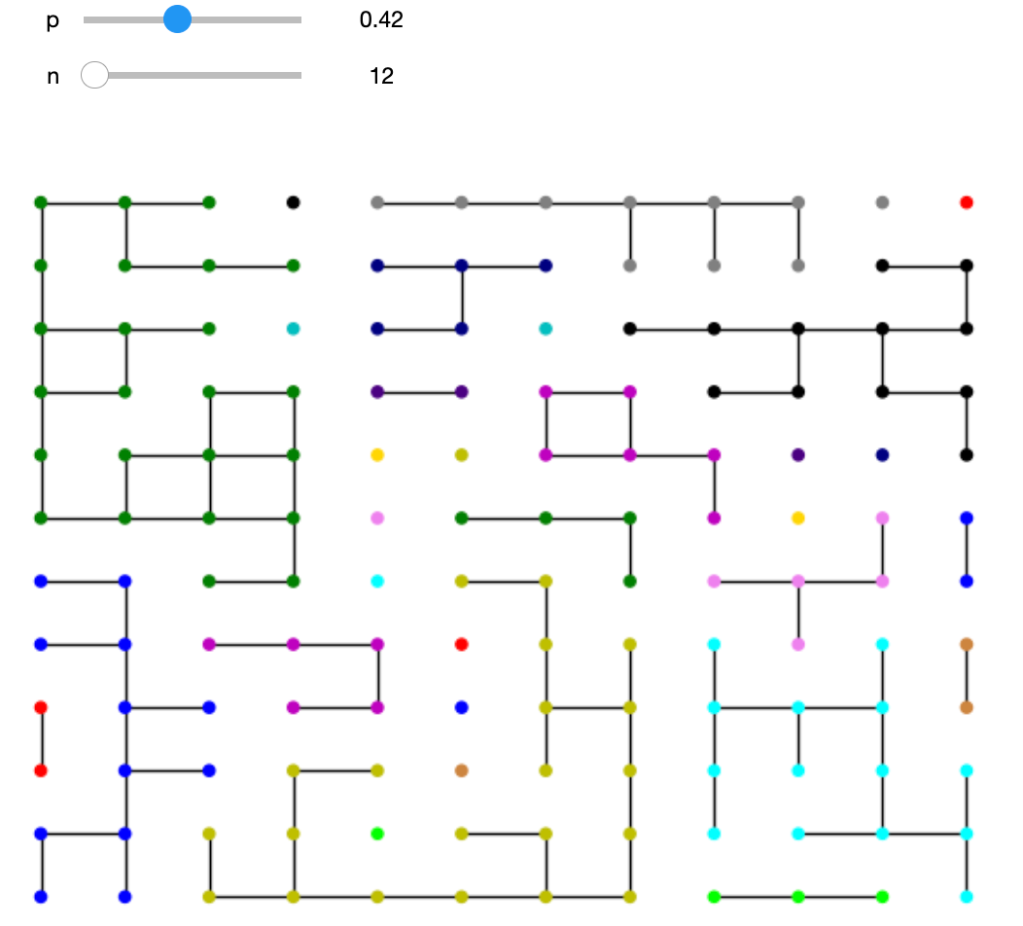
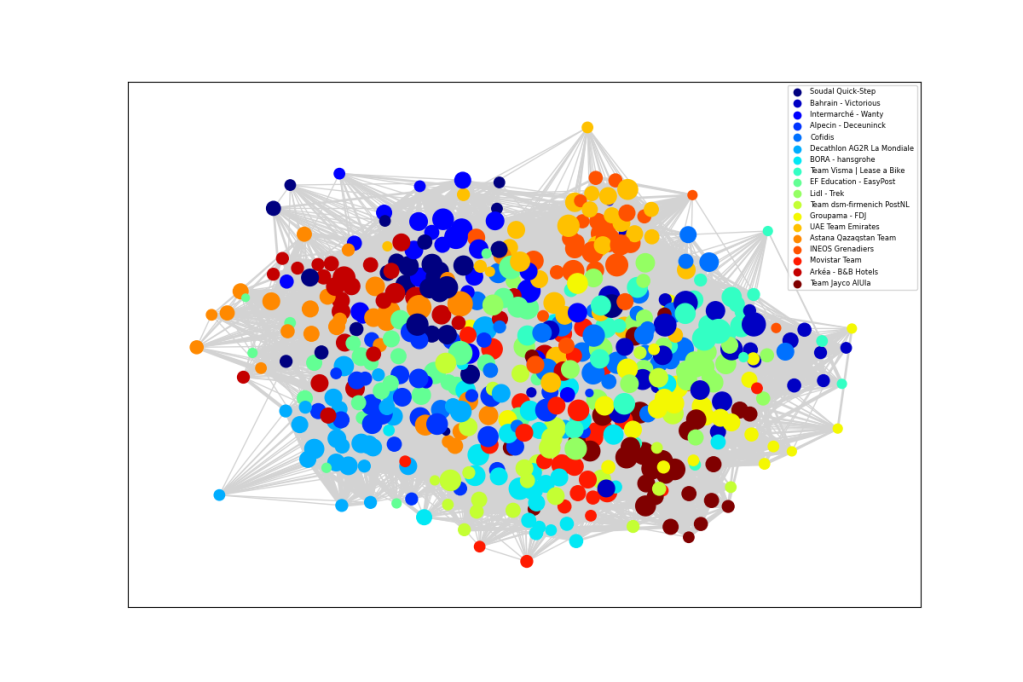
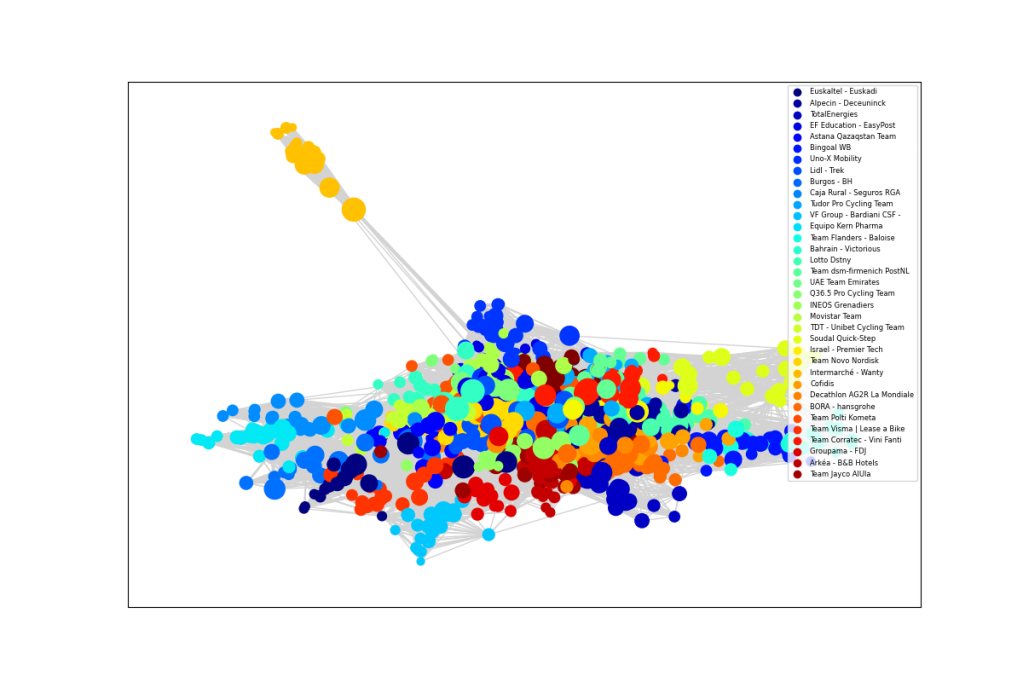
The resulting graphical network, displayed at the top of this blog, has some interesting properties that reveal the dynamics of professional cycling. The 18 world tour teams are displayed in different colours. The size of each rider node is scaled by length of career. An experienced rider, like Geraint Thomas, has a larger node and more connections, which are shown as light grey lines, where the thickness represents years in the pair of riders were in the same team. Newer riders, with fewer connections tend to be on the periphery. For example, Isaac del Toro is the orange UAE Team Emirates rider at the top.

There are no fixed rules about how to represent the network, but the idea is that more closely related riders ought to congregate together. The network shows INEOS near UAE as shades of orange in the top right. Next we have Team Visma Lease a Bike in cyan, around two o’clock, close to Lidl – Trek in light green, Bahrain – Victorious in darker blue and Cofidis in lighter blue. Yellow Groupama – FDJ lies above the dark brown Jayco AlUla riders in the lower right. Red Movistar, light green Team dsm-firmenich PostNLand light blue BORA – Hansgrohe are near 6 o’clock, though Primož Roglič lies much closer to his old team. Decathlon AG2R La Mondiale is light blue in the lower left, near the darker blue of Alpecin – Deceuninck and pale green EF Education – EasyPost. Astana is orange, around nine o’clock. Dark blue Soudal Quick-Step, lighter blue Intermarché – Wanty and red Arkéa – B&B Hotels all hover around the top left. Teams that are more dispersed would be indicative of higher annual turnover.

3 degrees of separation

No rider is more than three steps from any other. In fact the average distance between riders is two steps, because the chances are that two riders have ridden with someone in common over their careers. Although the neo-pros are obviously more distantly connected, Isaac del Toro rides with Adam Yates, who spent six years alongside Jack Haig at Michelton Scott, but who now rides for Bahrain Victorious as a teammate of Finlay Pickering.

Bob Jungels is the most connected rider, having been a teammate of 100 riders in the current peloton. Since 2012, he has ridden for five different teams. He and Florian Senechal are only two steps from all riders. The Polish rider Łukasz Wiśniowski has been with six teams and has 94 links. Then we have Mark Cavendish with 91 and Rui Costa with 89.

In contrast, taking account of spending multiple years as teammates, Geraint Thomas tops the list with 218 teammate years. Interestingly, he is followed by Jonathan Castroviejo, Salvatore Puccio, Michal Kwiatkowski, Luke Rowe, Ben Swift, all long-time colleagues at INEOS Grenadiers. This suggests they are very happy (or well paid) staying where they are.

If we estimate “long-term team loyalty” by number of teammate years divided by number teammates, Geraint is top, followed by Salvatore Puccio, Michael Hepburn, Luke Durbridge, Luke Rowe, Simon Yates and Jasper Stuyven.

Best buddies

The riders who have been teammates for the longest are Luke Durbridge/ Michael Hepburn and Robert Gesink/Steven Kruijswijk both 15 years,
Geraint Thomas has ridden with Ben Swift and Salvatore Puccio for 14 years and Luke Rowe with Salvatore Puccio for 13.

Outliers

In a broader analysis that includes all the Pro Continental teams alongside the World Tour, the graph below shows a notable team of outliers. This is Team Novo Nordisk for athletes who compete with type 1 diabetes. Their Hungarian rider, Peter Kusztor, was the teammate of several current riders, such as Jan Tratnik, prior to joining Novo Nordisk, in a career that stretches back to 2006. The team is an inspiration to everyone affected by diabetes.

Analysis

This analysis was performed in Python, using the NetworkX library.

Code can be found here.

How many heartbeats?

The fascinating work of Geoffrey West explores the idea of universal scaling laws. He describes how the lifetimes of organisms tend to increase with size: elephants live longer than mice. On the other hand, average heart rate tends to decrease with size. It turns out that these two factors balance each other in such as way that over their lifetimes, elephants have roughly the same number of heartbeats as mice and all other animals: about 1.5 billion.

Less active people might be tempted to suggest that indulging in exercise reduces our lifetimes, because we use up our allocation of heartbeats more quickly. However, exercisers tend to have a lower resting heart rate than their sedentary peers. So if we really had a fixed allocation of heartbeats, would we be better off exercising or not?

Power laws

To get a sense of how things change with scale, consider doubling the size of an object. Its surface area goes up 4 times (2 to the power of 2), while its volume and its mass rise 8 times (2 to the power of 3). Since an animal loses heat through its skin whereas its ability to generate heat depends on its muscle mass, larger animals are better able to survive a cold winter. This fact led some scientists to suspect that metabolism should be related to mass raised to the power of 2/3. However, empirical work by Max Klieber in the 1930s found a power exponent of 3/4 across a wide range of body sizes.

Geoffrey West went on to explain the common occurrence of the 1/4 factor in many power laws associating physiological characteristics with the size of biological systems. His work suggests that this is because, as they evolved, organisms have been subject to the constraints of living in a 3-dimensional world. The factor, 4, drops out of the analysis, being one more than the number of dimensions.

Two important characteristics are lifetime, which tends to increase in relation to mass raised to the power of 1/4, and heart rate, which is associated with mass raised to the power of -1/4. If you multiply the two together to obtain the total number of heartbeats, the 1/4 and the -1/4 cancel each other out, leaving you with a constant of around 1.5 billion.

Human heart beats

According to the NHS, the normal adult heart rate while resting is 60 to 100 bpm, but fitter people have lower heart rates, with athletes having rates of 40 to 60 bpm. Suppose we compare Lazy Larry, whose resting heart rate is 70bpm, with Sporty Steve, who has the same body mass, but has a resting heart rate of 50bpm.

Let’s assume that as Larry eats, drinks coffee and moves around, his average heart rate across the day is 80bpm. Steve carries out the same activities, but he also follows a weekly training plan of that involves periods of elevated heart rates. During exercise Steve’s heart beats at 140bpm for an average of one hour a day, but the rest time it averages 60bpm.

If Larry expects to live until he is 80, he would have 80*60*24*365*80 or 3.36 billion heart beats. This is higher than West’s figure of 1.5 billion, but before the advent of modern hygiene and medicine, it would not be unusual for humans to die by the age of 40.

Exercise is good for you

The key message is that, accounting for exercise, Steve’s average daily heart rate is (140*1+60*23)/24 or 63bpm. The benefits of having a lower heart rate than Larry easily offset the effects of one hour of daily vigorous exercise.

Although it is a rather silly exercise, one could ask how long Steve would live if he expected the same number of heartbeats as Larry. The answer is 80/63 times longer or 101 years. So if mortality were determined only by the capacity of the heart to beat a certain number of times, taking exercise could add 21 years to a lifetime. Before entirely dismissing that figure, note that NHS data show that ischaemic heart disease remains one of the leading causes of death in the UK. Cardiac health is a very important aspect of overall health.

Obviously many other factors affect longevity, for example those taking exercise tend to be more aware of their health and are less likely to suffer from obesity, smoke, consume excessive alcohol or eat ultra-processed foods.

A study of 4,082 Commonwealth Games medallists showed that male athletes gained between 4.5 and 5.3 extra years of life and female athletes 3.9. Although cycling was the only sport that wasn’t associated with longer lives, safety has improved and casualty rates have declined over the years.

Exercise, good nutrition and sufficient sleep are crucial for health and longevity. There’s no point in waiting until you are 60 and taking elixirs and magic potions. The earlier in life you adopt good habits, the longer you are likely to live.

Fuelling your rides on Strava

As we move into our 40s, 50s and beyond, we may become aware of changes in our bodies. Performance peaks level off or start to decline. Even if you don’t feel old, it becomes harder to keep up with younger sprinters. It takes longer to recover from a hard ride, injury or illness.

Muscle, Fat and Bone

The cause of these age-related changes is a decline in the production of specific hormones. Growth hormone falls insidiously from the time we reach adult height. From the age of 50, testosterone levels drop slightly in men, while oestradiol levels fall dramatically as women reach menopause. The key thing to note about growth hormone and testosterone is that they are anabolic agents, i.e. they build muscle. As they decline, there is a tendency to lose muscle and to increase fat deposition. Sex steroids also play a pivotal role in bone formation.

Protein, Carbohydrates and Vitamin D

Fortunately there are measures we can take to counter the effects of declining hormones. Nutrition plays an important role. Understanding the physiological effects of hormonal changes makes it easier to recognise beneficial adaptations in your diet.

Protein provides the building blocks required for muscle. Taking an adequate level of protein, spread out through the day, is beneficial.

Carbohydrates are the key fuel for moderate to high intensity. Fasted training is not advisable. The body’s shock reaction to underfuelled training is to deposit fat.

The UK government advises everyone to take vitamin D supplements, especially over the winter. In addition to supporting bone health, studies have shown improved immunity and muscle recovery.

Nutrition, Exercise and Recovery

When combined with adequate nutrition, exercise, particularly strength training, stimulates the production of growth hormone and testosterone. It is important to ensure adequate recovery and to follow a regular routine of going to be early, because these hormones are produced while you are asleep.

Everybody is unique, so you need to work out what works best for you. For further insights on this topic, Dr Nicky Keay has written a book full of top tips, called Hormones Health and Human Potential.

Generating music videos using Stable Diffusion

Video generated using Stable Diffusion

In my last post I described how to generate a series of images by feeding back the output of a Stable Diffusion image-to-image model as the input for the next image. I have now developed this into a Generative AI pipeline that creates music videos from the lyrics of songs.

Learning to animate

In my earlier blog about dreaming of the Giro, I saved a series of key frames in a GIF, resulting in an attractive stream of images, but the result was rather clunky. The natural next step was to improve the output by inserting frames to smooth out the transitions between the key frames, saving the result as a video in MP4 format, at a rate of 20 frames per second.

I started experimenting with a series of prompts, combined with the styles of different artists. Salvador Dali worked particularly well for dreamy animations of story lines. In the Dali example below, I used “red, magenta, pink” as a negative prompt to stop these colours swamping the image. The Kandinsky and Miro animations became gradually more detailed. I think these effects were a consequence of the repetitive feedback involved in the pipeline. The Arcimboldo portraits go from fish to fruit to flowers.

Animations in the styles of Dali, Kandinsky, Miro and Arcimboldo

Demo app

A created a demo app on Hugging Face called AnimateYourDream. In order to get this to work, you need to duplicate it and then run it using a GPU on your Hugging Face account (costing $0.06 per hour). The idea was to try to recreate a dream I’d had the previous night. You can choose the artistic style, select an option to zoom in, enter three guiding prompts with the desired number of frames and choose a negative prompt. The animation process takes 3-5 minutes on a basic GPU.

For example, setting the style as “Dali surrealist”, zooming in, with 5 frames each of “landscape”, “weird animals” and “a castle with weird animals” produced the following animation.

Demo of my AnimateYourDream app on Hugging Face

Music videos

After spending some hours generating animations on a free Google Colab GPU and marvelling over the animations, I found that the images were brought to life by the music I was playing in the background. This triggered the brainwave of using the lyrics of songs as prompts for the Stable Diffusion model.

In order to produce an effective music video, I needed the images to change in time with the lyrics. Rather than messing around editing my Python code, I ended up using a Excel template spreadsheet as a convenient way to enter the lyrics alongside the time in the track. It was useful to enter “text” as a negative prompt and a sometimes helpful to mention a particular colour to stop it dominating the output. By default an overall style is added to each prompt, but it is convenient to change the style on certain prompts. By default the initial image is used as a “shadow”, which contributes 1% to every subsequent frame, in an attempt to retain an overall theme. This can also be overridden on each prompt.

Finally, it was very useful to be able to define target images. If defined for the initial prompt, this saves loading an additional Stable Diffusion text-to-image pipeline to create the first frame. Otherwise, defining a target image for a particular prompt drags the animation towards the target, by mixing increasing proportions of the target with the current image, progressively from the previous prompt. This is also useful for the final frame of the animation. One way to create target images is to run a few prompts through Stable Diffusion here.

Although some lyrics explicitly mention objects that Stable Diffusion can illustrate, I found it helps to focus on specific key words. This is my template for “No more heroes” by The Stranglers. It produced an awesome video that I put on GitHub.

Once an Excel template is complete, the following pipeline generates the key frames by looping through each prompt and calculating how many frames are required to fill the time until the next prompt for the desired seconds per frame. A basic GPU takes about 3 seconds per key frame, so a song takes about 10-20 minutes, including inserting a smoothing steps between the key frames.

Sample files and a Jupyter notebook are posted on my GitHub repository.

I’ve started a YouTube channel

Having previously published my music on SoundCloud, I am now able to generate my own videos. So I have set up a YouTube channel, where you can find a selection of my work. I never expected the fast.ai course to lead me here.

PyData London

I presented this concept at the PyData London – 76th meetup on 1 August 2023. These are my slides.

Dreaming of the Giro

fast.ai’s latest version of Practical Deep Learning for Coders Part 2 kicks off with a review of Stable Diffusion. This is a deep neural network architecture developed by Stability AI that is able to convert text into images. With a bit of tweaking it can do all sorts of other things. Inspired by the amazing videos created by Softology, I set out to generate a dreamlike video based on the idea of riding my bicycle around a stage of the Giro d’Italia.

Text to image

As mentioned in a previous post, Hugging Face is a fantastic resource for open source models. I worked with one of fast.ai’s notebooks using a free GPU on Google Colab. In the first step I set up a text-t0-image pipeline using a pre-trained version of stable-diffusion-v1-4. The prompt “a treelined avenue, poplars, summer day, france” generated the following images, where model was more strongly guided by the prompt in each row. I liked the first image in the second row, so I decided to make this the first frame in an initial test video.

Stable diffusion is trained in a multimodal fashion, by aligning text embeddings with the encoded versions corresponding images. Starting with random noise, the pixels are progressively modified in order to move the encoding of the noisy image closer to something that matches the embedding of the text prompt.

Zooming in

The next step was to simulate the idea of moving forward along the road. I did this by writing a simple two-line function, using fast.ai tools, that cropped a small border off the edge of the image and then scaled it back up to the original size. In order to generate my movie, rather that starting with random noise, I wanted to use my zoomed-in image as the starting point for generating the next image. For this I needed to load up an image-to-image pipeline.

I spent about an hour experimenting with with four parameters. Zooming in by trimming only a couple of pixels around the edge created smoother transitions. Reducing the strength of additional noise enhanced the sense of continuity by ensuring that that subsequent images did not change too dramatically. A guidance scale of 7 forced the model to keep following prompt and not simply zoom into the middle of the image. The number of inference steps provided a trade-off between image quality and run time.

When I was happy, I generated a sequence of 256 images, which took about 20 minutes, and saved them as a GIF. This produced a pleasing, constantly changing effect with an impressionist style.

Back to where you started

In order to make the GIF loop smoothly, it was desirable to find a way to return to the starting image as part of the continuous zooming in process. At first it seemed that this might be possible by reversing the existing sequence of images and then generating a new sequence of images using each image in the reversed list as the next starting point. However, this did not work, because it gave the impression of moving backwards, rather than progressing forward along the road.

After thinking about the way stable diffusion works, it became apparent that I could return to the initial image by mixing it with the current image before taking the next step. By progressively increasing the mixing weight of the initial image, the generated images became closer to target over a desired number of steps as shown below.

Putting it al together produced the following video, which successfully loops back to its starting point. It is not a perfect animation, because the it zooms into the centre, whereas the vanishing point is below the centre of the image. This means we end up looking up at the trees at some points. But overall it had the effect I was after.

A stage of the Giro

Once all this was working, it was relatively straightforward to create a video that tells a story. I made a list of prompts describing the changing countryside of an imaginary stage of the Giro d’Italia, specifying the number of frames for each sequence. I chose the following.

[‘a wide street in a rural town in Tuscany, springtime’, 25],

[‘a road in the countryside, in Tuscany, springtime’,25],

[“a road by the sea, trees on the right, sunny day, Italy”,50],

[‘a road going up a mountain, Dolomites, sunny day’,50],

[‘a road descending a mountain, Dolomites, Italy’,25],

[‘a road in the countryside, cypress trees, Tuscany’,50],

[‘a narrow road through a medieval town in Tuscany, sunny day’,50]

These prompts produced the video shown at the top of this post. The springtime blossom in the starting town was very effective and the endless climb up into the sunlit Dolomites looked great. For some reason the seaside prompt did not work, so the sequence became temporarily stuck with red blobs. Running it again would make something different. Changing the prompts offered endless possibilities.

The code to run this appears on my GitHub page. If you have a Google account, you can open it directly in Colab and set the RunTime to GPU. You also need a free Hugging Face account to load the stable diffusion pipelines.

Percolating Python with ChatGPT

A YouTube video about “percolation” includes an interesting animation of shifting colours that exhibits a sudden phase transition. As a challenge, I set out to replicate the evolving pattern in Python. But then I remembered hearing that ChatGPT was good at writing code, so I asked it for help

Percolation

Percolation models can be used to simulate physical systems, such as liquids permeating through porous materials. The idea is to take a grid pattern of nodes with edges between them, and then remove edges at random. Each edge survives with a probability, p. If the edges were pipes, we could imagine that water could percolate through a well-connected grid (image on the left), but, as more edges are removed, the nodes form connected islands that prevent onward percolation (image on the right).

Asking ChatGPT

I started by asking ChatGPT to model a randomly connected lattice in Python. It suggested using a library called networkx that I have used in the past, so I pasted the code into a Jupyter notebook. The code worked, but the nodes were scattered at random, so I asked ChatGPT for code to produce a regular grid. This failed, so I passed the error message back to ChatGPT, which explained the problem and suggested revised code that worked perfectly, producing something like the left hand image above.

The next step was to apply the same colour to all connected nodes. Initially I called these clusters, but then I discovered that networkx has a method called connected_components, so I substituted this into ChatGPT’s code. After about half an hour, I had added more colours and some ipywidget sliders, to produce a fully working interactive model, where I could vary p and adjust the size of the grid.

The really interesting behaviour happens when p is around 0.5. Below this value the grid tends to form a disjoint set of unconnected islands, but above the critical value, the large areas quickly connect up. This image at the top of this blog occurs around the middle of the video below.

Percolation Model

Python code

This is the code if you want to try it yourself. You might need to pip install networkx and ipywidgets.

import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
import random
from ipywidgets import interact

def randomLattice(p=0.5, n = 100):
    # Square grid m=n
    m=n
    # Create a 2D grid of nodes using NumPy
    nodes = np.array([(i, j) for i in range(m) for j in range(n)])

    # Convert the NumPy array to a list of tuples
    nodes = [tuple(node) for node in nodes]

    # Create an empty graph
    G = nx.Graph()

    # Add nodes to the graph
    G.add_nodes_from(nodes)

    # Connect adjacent nodes horizontally
    for i in range(m):
        for j in range(n-1):
            if random.random() < p:  # adjust the probability to control the connectivity
                G.add_edge((i, j), (i, j+1))

    # Connect adjacent nodes vertically
    for i in range(m-1):
        for j in range(n):
            if random.random() < p:  # adjust the probability to control the connectivity
                G.add_edge((i, j), (i+1, j))


    clusters = list(nx.connected_components(G))
    colours = ["b", "r", "g", "y", "m", "c", "k",'lime','cyan','violet','gold','indigo','navy','grey','peru']
    node_to_colour = {}
    for i, cluster in enumerate(clusters):
        for node in cluster:
            node_to_colour[node] = colours[i%len(colours)]
    #print(clusters)
    # Draw the graph as a regular grid
    pos = dict(zip(nodes, nodes))
    nx.draw(G, pos=pos, node_color=[node_to_colour[i] for i in nodes], 
            with_labels=False,node_size=20)
    #plt.savefig(f'Grid_{int(p*100):03d}.png')
    plt.show()
    return


interact(randomLattice,p=(0,1,0.01), n = (5,200,1));