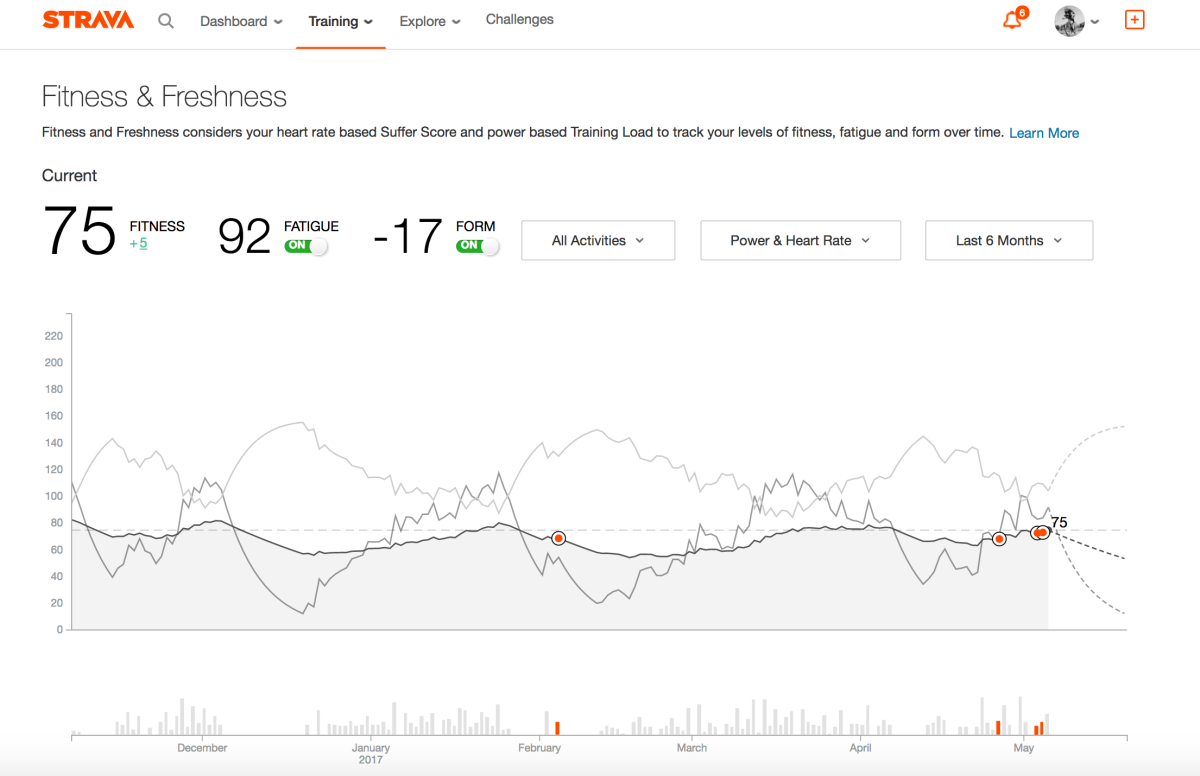
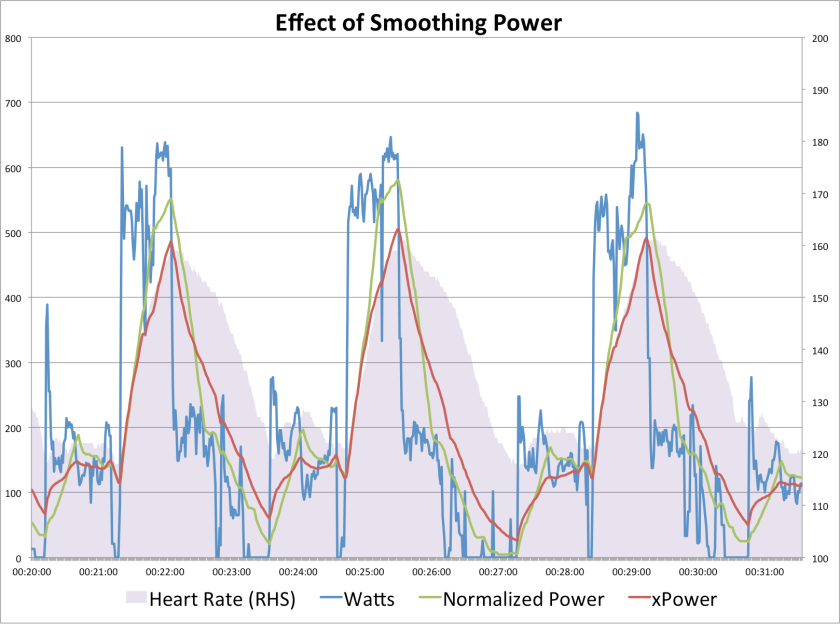
When you upload a ride, Strava draws a map using the longitude and latitude coordinates recorded by your GPS device. This article explores ways in which these numbers, along with other metrics, can be used to create interesting images that might have some artistic merit.
The idea was motivated by the huge advances made in the field of Deep Learning, particularly applications for image recognition. However, since datasets come in all shapes and forms, researchers have explored ways of converting different types of data into images. In a paper published in 2015, the authors achieved success in identifying standard time series by converting them into images.
GPS bike computers typically record snapshots of information every second. What kind of images could these time series generate? It turns out that there are several ways to convert a time series into an image.
Spectrogram
Creating a spectrogram is a standard approach from signal processing that is particularly useful for analysing acoustic files. The spectrogram is a heat map that shows how the underlying frequencies contributing to the signal change over time. Technically, it is derived by calculating the discrete Fourier transform of a window that slides across the time series. I applied this to my regular Saturday morning club ride of four laps around Richmond Park. The image changes a bit once the ride gets going after about 1200 seconds (20 minutes), but, frankly, the result was not particularly illuminating. There is no obvious reason to consider cycling power data as a superposition of frequencies.

Ah! Now we are getting somewhere
The authors of the referenced paper took a different approach to produce things called Gramian Angular Summation Field (GASF), Gramian Angular Difference Field (GADF), and Markov Transition Field (MTF). Read the paper if want to know the details. I created these and something call a Recurrence Plot. All of these methods generate a matrix, by combining every element in the time series with every other element. The underling observations occurring at times and
determine the colour of the pixel at position (
,
). Images are symmetric along the lower-left to upper-right diagonal, apart from GADF, which is antisymmetric.
Let’s see how do they look for on four laps of Richmond Park. We have six time series, with corresponding sets of images below. The segmentation of the images is due to periodicity of the data. This is particularly clear in the geographic data (longitude, latitude and altitude). The higher intensity of the main part of the ride is most obvious in the heart rate data. The MTF plots are quite interesting. Scroll down through the images to the next section





From cycle ride to art
It is one thing to create an image of each item, but how can we combine these to summarise a ride in a single image. I considered two methods of combining time series into a single image: a) create a new image where the vertical and horizontal axes represent different series and b) create a new image by simply adding the corresponding values from two underlying images.
One problem is that some cyclists don’t have gadgets like heart rate monitors and power meters, so I initially restricted myself to just the longitude, latitude and altitude data. Nevertheless, as noted in an earlier blog, it is possible to work out speed, because the time interval is one second between each reading. Furthermore, one can estimate power, from the speed and changes in elevation.
Another problem is that rides differ in length. For this I split the ride into, say, 128 intervals and took the last observation in each interval. So for a 3 hour ride, I’d be sampling about once every 84 seconds.
The chart at the top of this blog was created by first normalising each series to a standard range (-1, +1). Method a) was used to create two images: longitude was added to latitude and altitude was multiplied by speed. These were added using method b). Using these measures will produce pretty much the same chart each time the ride is done. In contrast, an image that is totally unique to the ride can be produced using data relating to the individual rider. The image below uses the same recipe to combine speed, heart rate, power and cadence. If this had been a particularly special ride, the image would be a nice personal memento.

For anyone interested in the underlying code, I have posted a Jupyter notebook here.
References
Encoding Time Series as Images for Visual Inspection and Classification Using Tiled Convolutional Neural Networks, Wang Z Oates T, https://www.aaai.org/ocs/index.php/WS/AAAIW15/paper/viewFile/10179/10251


 This is a common problem in signal processing, where the
This is a common problem in signal processing, where the 
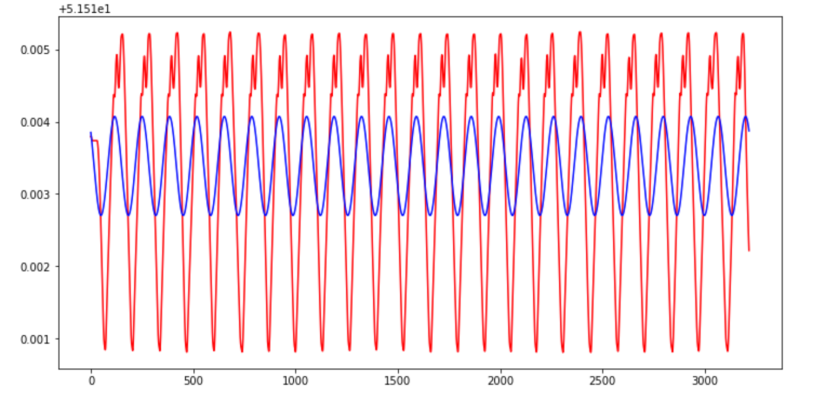






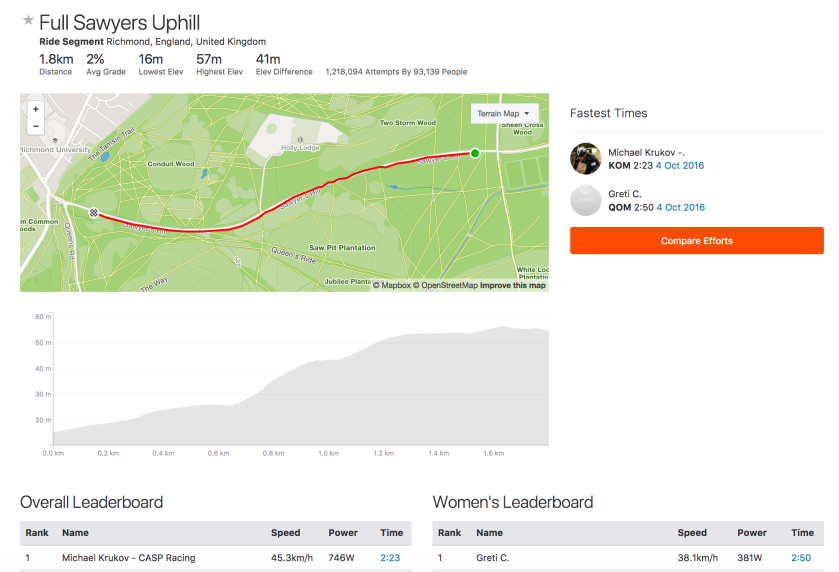


 It is relatively straightforward to show that the triangulation method will underestimate both distance and speed by a factor of 2r/s*sin(s/2r), where r is the radius of the corner in metres and s is speed in m/s. So the estimated length of the 20m arc for the fast rider is 19.4m ridden at a speed of 35.1km/h (2.5% underestimate), while the corresponding figures for the slower rider would be 19.8m at 17.9km/h (0.6% underestimate).
It is relatively straightforward to show that the triangulation method will underestimate both distance and speed by a factor of 2r/s*sin(s/2r), where r is the radius of the corner in metres and s is speed in m/s. So the estimated length of the 20m arc for the fast rider is 19.4m ridden at a speed of 35.1km/h (2.5% underestimate), while the corresponding figures for the slower rider would be 19.8m at 17.9km/h (0.6% underestimate).