Data Science – Science4Performance

Cyclo-Social Networks

When Mexico’s Isaac del Toro and the Brit, Finlay Pickering, joined World Tour teams in 2024, they became part of an elite group. The structure of the professional cycling community differs from other types of social network, because the sport is organised around close-knit teams. You may have heard of the idea that everyone in the world is connected by six degrees of separation. Many social networks include key individuals who act as hubs linking disparate groups. How closely connected are professional cyclist? Which cyclists are the most connected?

Forming a link

An obvious way for cyclists to become acquainted is by being part of the same team. They spend long periods travelling, training, eating and relaxing together, often sharing rooms. Working as a team through the trials and tribulations of elite competition develops high degrees of camaraderie.

Each rider’s page on ProCyclingStats includes a team history. So I checked the past affiliations of all the current UCI world team riders. The idea was to build a graph where each node represented a rider, with edges connecting riders who had been in the same team. Each edge was weighted by the number of years a pair of riders had been in the same team, reflecting the strength of their relationship.

Cyclo-social network

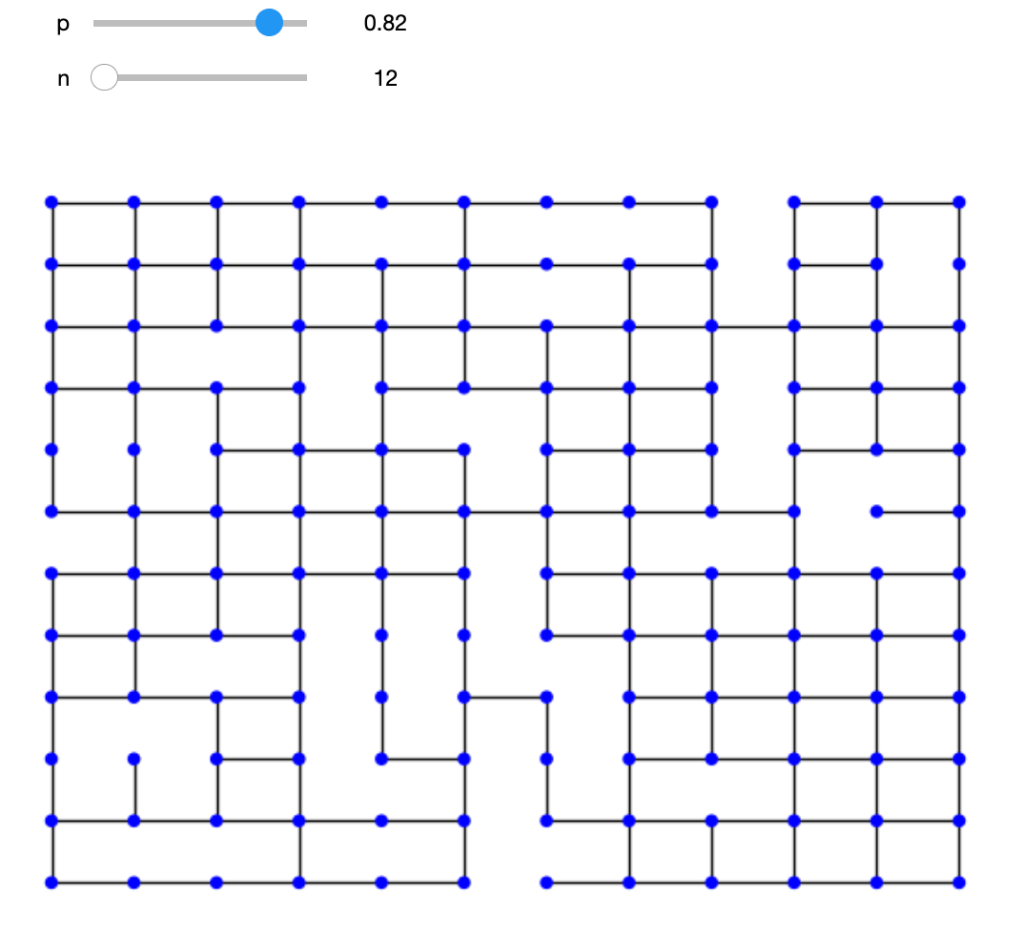
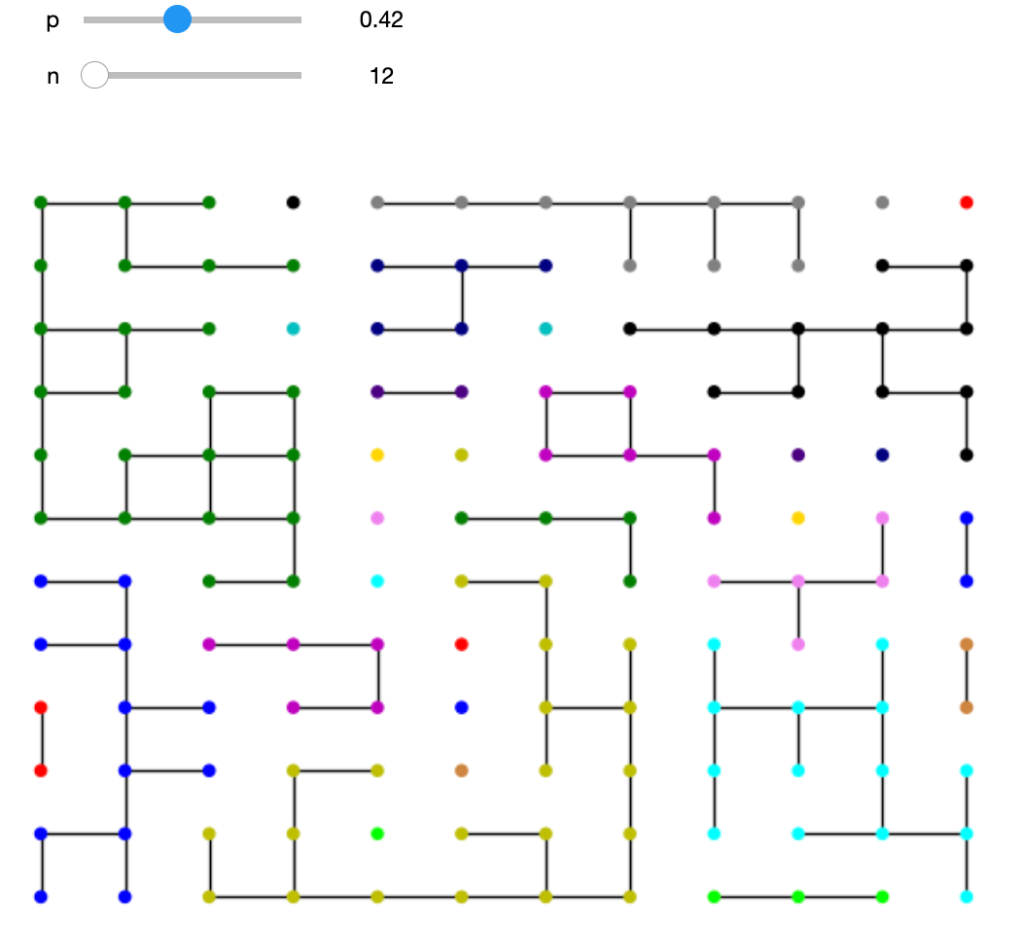
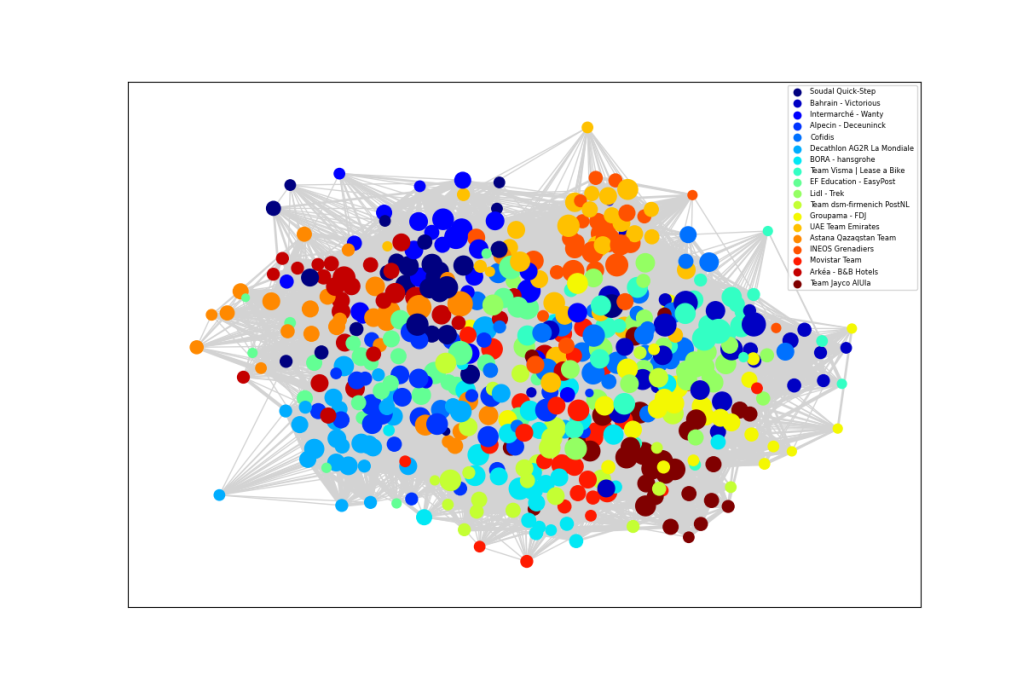
The resulting graphical network, displayed at the top of this blog, has some interesting properties that reveal the dynamics of professional cycling. The 18 world tour teams are displayed in different colours. The size of each rider node is scaled by length of career. An experienced rider, like Geraint Thomas, has a larger node and more connections, which are shown as light grey lines, where the thickness represents years in the pair of riders were in the same team. Newer riders, with fewer connections tend to be on the periphery. For example, Isaac del Toro is the orange UAE Team Emirates rider at the top.

There are no fixed rules about how to represent the network, but the ideas is that more closely related riders ought to congregate together. The network shows INEOS near UAE as shades of orange in the top right. Next we have Team Visma Lease a Bike in cyan, around two o’clock, close to Lidl – Trek in light green, Bahrain – Victorious in darker blue and Cofidis in lighter blue. Yellow Groupama – FDJ lies above the dark brown Jayco AlUla riders in the lower right. Red Movistar, light green Team dsm-firmenich PostNLand light blue BORA – Hansgrohe are near 6 o’clock, though Primož Roglič lies much closer to his old team. Decathlon AG2R La Mondiale is light blue in the lower left, near the darker blue of Alpecin – Deceuninck and pale green EF Education – EasyPost. Astana is orange, around nine o’clock. Dark blue Soudal Quick-Step, lighter blue Intermarché – Wanty and red Arkéa – B&B Hotels all hover around the top left. Teams that are more dispersed would be indicative of higher annual turnover.

3 degrees of separation

No rider is more than three steps from any other. In fact the average distance between riders is two steps, because the chances are that two riders have ridden with someone in common over their careers. Although the neo-pros are obviously more distantly connected, Isaac del Toro rides with Adam Yates, who spent six years alongside Jack Haig at Michelton Scott, but who now rides for Bahrain Victorious as a teammate of Finlay Pickering.

Bob Jungels is the most connected rider, having been a teammate of 100 riders in the current peloton. Since 2012, he has ridden for five different teams. He and Florian Senechal are only two steps from all riders. The Polish rider Łukasz Wiśniowski has been with six teams and has 94 links. Then we have Mark Cavendish with 91 and Rui Costa with 89.

In contrast, taking account of spending multiple years as teammates, Geraint Thomas tops the list with 218 teammate years. Interestingly, he is followed by Jonathan Castroviejo, Salvatore Puccio, Michal Kwiatkowski, Luke Rowe, Ben Swift, all long-time colleagues at INEOS Grenadiers. This suggests they are very happy (or well paid) staying where they are.

If we estimate “long-term team loyalty” by number of teammate years divided by number teammates, Geraint is top, followed by Salvatore Puccio, Michael Hepburn, Luke Durbridge, Luke Rowe, Simon Yates and Jasper Stuyven.

Best buddies

The riders who have been teammates for the longest are Luke Durbridge/ Michael Hepburn and Robert Gesink/Steven Kruijswijk both 15 years,
Geraint Thomas has ridden with Ben Swift and Salvatore Puccio for 14 years and Luke Rowe with Salvatore Puccio for 13.

Outliers

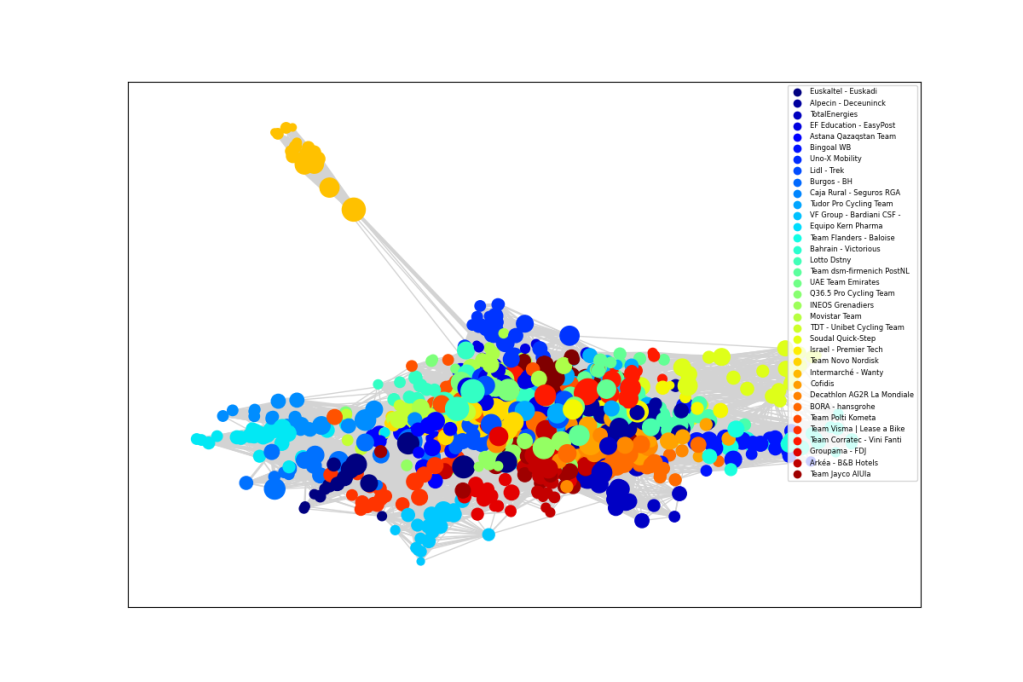
In a broader analysis that includes all the Pro Continental teams alongside the World Tour, the graph below shows a notable team of outliers. This is Team Novo Nordisk for athletes compete with type 1 diabetes. Their Hungarian rider, Peter Kusztor, was the teammate of several current riders, such as Jan Tratnik, prior to joining Novo Nordisk, in a career that stretches back to 2006. The team is an inspiration to everyone affected by diabetes.

Analysis

This analysis was performed in Python, using the NetworkX library.

Code can be found here.

Generating music videos using Stable Diffusion

Video generated using Stable Diffusion

In my last post I described how to generate a series of images by feeding back the output of a Stable Diffusion image-to-image model as the input for the next image. I have now developed this into a Generative AI pipeline that creates music videos from the lyrics of songs.

Learning to animate

In my earlier blog about dreaming of the Giro, I saved a series of key frames in a GIF, resulting in an attractive stream of images, but the result was rather clunky. The natural next step was to improve the output by inserting frames to smooth out the transitions between the key frames, saving the result as a video in MP4 format, at a rate of 20 frames per second.

I started experimenting with a series of prompts, combined with the styles of different artists. Salvador Dali worked particularly well for dreamy animations of story lines. In the Dali example below, I used “red, magenta, pink” as a negative prompt to stop these colours swamping the image. The Kandinsky and Miro animations became gradually more detailed. I think these effects were a consequence of the repetitive feedback involved in the pipeline. The Arcimboldo portraits go from fish to fruit to flowers.

Animations in the styles of Dali, Kandinsky, Miro and Arcimboldo

Demo app

A created a demo app on Hugging Face called AnimateYourDream. In order to get this to work, you need to duplicate it and then run it using a GPU on your Hugging Face account (costing $0.06 per hour). The idea was to try to recreate a dream I’d had the previous night. You can choose the artistic style, select an option to zoom in, enter three guiding prompts with the desired number of frames and choose a negative prompt. The animation process takes 3-5 minutes on a basic GPU.

For example, setting the style as “Dali surrealist”, zooming in, with 5 frames each of “landscape”, “weird animals” and “a castle with weird animals” produced the following animation.

Demo of my AnimateYourDream app on Hugging Face

Music videos

After spending some hours generating animations on a free Google Colab GPU and marvelling over the animations, I found that the images were brought to life by the music I was playing in the background. This triggered the brainwave of using the lyrics of songs as prompts for the Stable Diffusion model.

In order to produce an effective music video, I needed the images to change in time with the lyrics. Rather than messing around editing my Python code, I ended up using a Excel template spreadsheet as a convenient way to enter the lyrics alongside the time in the track. It was useful to enter “text” as a negative prompt and a sometimes helpful to mention a particular colour to stop it dominating the output. By default an overall style is added to each prompt, but it is convenient to change the style on certain prompts. By default the initial image is used as a “shadow”, which contributes 1% to every subsequent frame, in an attempt to retain an overall theme. This can also be overridden on each prompt.

Finally, it was very useful to be able to define target images. If defined for the initial prompt, this saves loading an additional Stable Diffusion text-to-image pipeline to create the first frame. Otherwise, defining a target image for a particular prompt drags the animation towards the target, by mixing increasing proportions of the target with the current image, progressively from the previous prompt. This is also useful for the final frame of the animation. One way to create target images is to run a few prompts through Stable Diffusion here.

Although some lyrics explicitly mention objects that Stable Diffusion can illustrate, I found it helps to focus on specific key words. This is my template for “No more heroes” by The Stranglers. It produced an awesome video that I put on GitHub.

Once an Excel template is complete, the following pipeline generates the key frames by looping through each prompt and calculating how many frames are required to fill the time until the next prompt for the desired seconds per frame. A basic GPU takes about 3 seconds per key frame, so a song takes about 10-20 minutes, including inserting a smoothing steps between the key frames.

Sample files and a Jupyter notebook are posted on my GitHub repository.

I’ve started a YouTube channel

Having previously published my music on SoundCloud, I am now able to generate my own videos. So I have set up a YouTube channel, where you can find a selection of my work. I never expected the fast.ai course to lead me here.

PyData London

I presented this concept at the PyData London – 76th meetup on 1 August 2023. These are my slides.

Percolating Python with ChatGPT

A YouTube video about “percolation” includes an interesting animation of shifting colours that exhibits a sudden phase transition. As a challenge, I set out to replicate the evolving pattern in Python. But then I remembered hearing that ChatGPT was good at writing code, so I asked it for help

Percolation

Percolation models can be used to simulate physical systems, such as liquids permeating through porous materials. The idea is to take a grid pattern of nodes with edges between them, and then remove edges at random. Each edge survives with a probability, p. If the edges were pipes, we could imagine that water could percolate through a well-connected grid (image on the left), but, as more edges are removed, the nodes form connected islands that prevent onward percolation (image on the right).

Asking ChatGPT

I started by asking ChatGPT to model a randomly connected lattice in Python. It suggested using a library called networkx that I have used in the past, so I pasted the code into a Jupyter notebook. The code worked, but the nodes were scattered at random, so I asked ChatGPT for code to produce a regular grid. This failed, so I passed the error message back to ChatGPT, which explained the problem and suggested revised code that worked perfectly, producing something like the left hand image above.

The next step was to apply the same colour to all connected nodes. Initially I called these clusters, but then I discovered that networkx has a method called connected_components, so I substituted this into ChatGPT’s code. After about half an hour, I had added more colours and some ipywidget sliders, to produce a fully working interactive model, where I could vary p and adjust the size of the grid.

The really interesting behaviour happens when p is around 0.5. Below this value the grid tends to form a disjoint set of unconnected islands, but above the critical value, the large areas quickly connect up. This image at the top of this blog occurs around the middle of the video below.

Percolation Model

Python code

This is the code if you want to try it yourself. You might need to pip install networkx and ipywidgets.

import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
import random
from ipywidgets import interact

def randomLattice(p=0.5, n = 100):
    # Square grid m=n
    m=n
    # Create a 2D grid of nodes using NumPy
    nodes = np.array([(i, j) for i in range(m) for j in range(n)])

    # Convert the NumPy array to a list of tuples
    nodes = [tuple(node) for node in nodes]

    # Create an empty graph
    G = nx.Graph()

    # Add nodes to the graph
    G.add_nodes_from(nodes)

    # Connect adjacent nodes horizontally
    for i in range(m):
        for j in range(n-1):
            if random.random() < p:  # adjust the probability to control the connectivity
                G.add_edge((i, j), (i, j+1))

    # Connect adjacent nodes vertically
    for i in range(m-1):
        for j in range(n):
            if random.random() < p:  # adjust the probability to control the connectivity
                G.add_edge((i, j), (i+1, j))


    clusters = list(nx.connected_components(G))
    colours = ["b", "r", "g", "y", "m", "c", "k",'lime','cyan','violet','gold','indigo','navy','grey','peru']
    node_to_colour = {}
    for i, cluster in enumerate(clusters):
        for node in cluster:
            node_to_colour[node] = colours[i%len(colours)]
    #print(clusters)
    # Draw the graph as a regular grid
    pos = dict(zip(nodes, nodes))
    nx.draw(G, pos=pos, node_color=[node_to_colour[i] for i in nodes], 
            with_labels=False,node_size=20)
    #plt.savefig(f'Grid_{int(p*100):03d}.png')
    plt.show()
    return


interact(randomLattice,p=(0,1,0.01), n = (5,200,1));

Active Inference

Active Inference is a fascinating and ambitious book. It describes a very general normative approach to understanding the mind, brain and behaviour, hinting at potential applications in machine learning and the social sciences. The authors argue that the ways in which living beings interact with the environment can be modelled in terms of something called the free energy principle.

Active Inference builds on the concept of a Bayesian Brain. This is the idea that our brains continually refine an internal model of the external world, acting as probabilistic inference machines. The internal generative model continually predicts the state of the environment and compares its predictions with the inputs of sensory organs. When a discrepancy occurs, the brain updates its model. This is called perception.

But Active Inference goes further my recognising that living things can interact with their environments. Therefore an alternative way to deal with a discrepancy versus expectations is to do something that modifies the world. This is called action.

Variational Free Energy

Active Inference, Parr, Pezzulo, Friston

Either you change your beliefs to match the world or you change the world to match your beliefs. Active Inference makes this trade off by minimising variational free energy, which improves the match between an organism’s internal model and the external world.

The theory is expressed in elegant mathematical terms that lend themselves to systematic analysis. Minimising variational free energy can be considered in terms of finding a maximum entropy distribution, minimising complexity or reducing the divergence between the internal model and the actual posterior distribution.

Expected free energy

Longer term planning is handled in terms of expected free energy. This is where the consequences of future sequences of actions (policies) are evaluated by predicting the outcomes at each stage. The expected free energy of each policy is converted into a score, with the highest score determining the policy the organism expects to pursue. The process of selecting policies that improve the match with the priors pertaining to favoured states is called learning.

Planning is cast in terms of Bayesian inference. Once again the algebraic framework lends itself to a range of interpretations. For example, it automatically trades off information gain (exploration) against pragmatic value (exploitation). This contrasts with reinforcement learning, which handles the issue more heuristically, by trial and error, combined with the notion of a reward.

Applications

The book describes applications in neurobiology, learning and perception. Although readers are encouraged to apply the ideas to new areas, a full understanding of the subject demands the dedication to battle through some heavy duty mathematical appendices, covering Bayesian inference, partially observed Markov Decision Processes and variational calculus.

Nevertheless the book is filled with thought provoking ideas about how living things thrive in the face of the second law of thermodynamics.

Milan Sanremo in a Random Forest

Predicted top ten for Milan San Remo 2021

Last time I tried to predict a race, I trained up a neural network on past race results, ahead of the World Championships in Harrogate. The model backed Sam Bennett, but it did not take account of the weather conditions, which turned out to be terrible. Fortunately the forecast looks good for tomorrow’s Milan Sanremo.

This time I have tried using a Random Forest, based on the results of the UCI races that took place in 2020 and so far in 2021. The model took account of each rider’s past results, team, height and weight, together with key statistics about each race, including date, distance, average speed and type of parcours.

One of the nice things about this type of model is that it is possible to see how the factors contribute to the overall predictions. The following waterfall chart explains why the model uncontroversially has Wout van Aert as the favourite.

Breakdown of prediction for Wout van Aert

The largest positive contribution comes from being Wout van Aert. This is because he has a lot of good results. His height and weight favour Milan Sanremo. He also has a strong positive coming from his team. This distance and race type make further positive contributions.

We can contrast this with the model’s prediction for Mathieu van der Poel, who is ranked 9th.

Breakdown of prediction for Mathieu van der Poel

We see a positive personal contribution from being van der Poel, but having raced fewer UCI events, he has less of a strong set of results than van Aert. According to the model the Alpecin Fenix team contribution is not a strong as Jumbo Visma, but the long distance of the race works in favour of the Dutchman. The day of year gives a small negative contribution, suggesting that his road results have been stronger later in the year, but this could be due to last year’s unusual timing of races.

Each of the other riders in the model’s top 10 is in with a shout.

It’s taken me all afternoon to set up this model, so this is just a short post.

Post race comment

Where was Jasper Stuyven?

Like Mads Pedersen in Harrogate back in 2019, Jasper Stuyven was this year’s surprise winner in Sanremo. So what had the model expected for him? Scrolling down the list of predictions, Stuyven was ranked 39th.

Breakdown of prediction for Jasper Stuyven

His individual rider prediction was negative, perhaps because he has not had many good results so far this year, though he did win Omloop Het Nieuwsblad last year and had several top 10 finishes. The model assessed that his greatest advantage came from the length of the race, suggesting that he tends to do well over greater distances.

The nice thing about this approach is that that it identifies factors that are relevant to particular riders, in a quantitative fashion. This helps to overcome personal biases and the human tendency to overweight and project forward what has happened most recently.

Hexagons in the Arctic Circle

An attractive aspect of hexagonal patterns is that they can repeat in interesting ways across a cycling jersey. This is partly due to the fact that a hexagon can be divided up into three equal lozenge shapes, as seen near the neck of the top right jersey. These shapes can be combined in imaginative ways, as displayed in the lower two examples.

This three-way division of a hexagon can create a 3D optical illusion called a “Necker cube”, which can appear to flip from convex to concave and back again. The orange patch can appear to be the top of a cube viewed from above or the ceiling in a corner, viewed from below. See if this happens if you stare at the image below.

Looking down on a cube or up into the corner of a room?

Spoiler alert: from here things gets a bit mathematical

Tessellations

A tessellation, or tiling, is a way of covering a plane with polygons of various types. Tessellations have many interesting mathematical properties relating to their symmetries. It turns out that there are exactly 17 types of periodic patterns. Roger Penrose, who was awarded the 2020 Nobel Prize in Physics for his work on the formation of black holes, discovered many interesting aperiodic tilings, such as the Penrose tiling.

While some people were munching on mince pies before Christmas, I watched a thought-provoking video on a related topic, released by the Mathologer, Burkard Polster. He begins by discussing ways of tiling various shapes with dominoes and goes on describe something called the Arctic Circle Theorem. Around the middle of the video, he shifts to tiling hexagon shapes with lozenges, resulting in images with the weird 3D flipping effect described above. This prompted me to spend rather a lot of time writing Python code to explore this topic.

After much experimentation, I created some code that would generate random tilings by stochastically flipping hexagons. Colouring the lozenges according to their orientation resulted in some really interesting 3D effects.

Algorithm flips a random hexagon to create a new tiling.

Neckered

The video shows random tilings of a hexagonal area. These end up looking like a collection of 3D towers with orange tops. But if you focus on a particular cube and tilt your screen backwards, the whole image can flip, Necker-style into an inverted version where the floor becomes the ceiling and the orange segments push downwards.

I used my code to create random tilings of much bigger hexagons. It turned out that plotting the image on every iteration was taking a ridiculous amount of time. Suspending plotting until the end resulted in the code running 10,000 time faster! This allowed me to run 50 million iterations for a hexagon with 32 lozenges on each size, resulting in the fabled Arctic Circle promised by the eponymous theorem. The central area is chaotic, but the colours freeze into opposite solid patches of orange, blue and grey outside the circumference of a large inscribed circle.

Arctic Circle emerged on a hexagon of side 32 after 50 million iterations

Why does the Arctic Circle emerge?

There are two intuitive ways to understand why this happens. Firstly, if you consider the pattern as representing towers with orange tops, then every tower must be taller than the three towers in front of it. So if you try to add or remove a brick randomly, the towers at the back are more likely to become taller, while those near the front tend to become shorter.

Two examples of paths from left to right

The second way to think about it is that, if you look carefully, there is a unique path from each of the lozenges on the left hand vertical side to the corresponding lozenge on the right hand vertical side. At every step, each path either goes up (blue) or down (grey). The gaps between the various paths are orange. Each step of the algorithm flips between up-down and down-up steps on a particular path. On the large hexagon, the only way to prevent the topmost cell from being orange is for the highest path to go up (and remain blue) 32 times in a row. This is very unlikely when flips are random, though it can happen more often on a smaller size-6 hexagon like the one shown in the example.

Resources

A Jupyter notebook demonstrating the approach and Python code for running longer simulations are available on this GitHub page.

Back to cycling jerseys

The Dutch company DSM is proudly sponsoring a professional cycling team in 2021. And a hexagon lies at the heart of the DSM logo, that will appear on the team jerseys.

Pro cycling team networks

The COVID-19 pandemic has further exposed the weakness of the professional cycling business model. The competition between the teams for funding from a limited number of sponsors undermines the stability of the profession. With marketing budgets under strain, more teams are likely to face difficulties, in spite of the great advertising and publicity that the sport provides. Douglas Ryder is fighting an uphill struggle trying to keep his team alive after the withdrawal of NTT as a lead sponsor. One aspect of stability is financial, but another measure is the level of transfers between teams.

The composition of some teams is more stable than others. This is illustrated by analysing the history of riders’ careers, which is available on ProCyclingStats. The following chart is a network of the transfers between teams in the last year, where the yellow nodes are 2020 teams and the purple ones are 2019. The width of the edges indicates how many riders transferred between the teams, with the thick green lines representing the bulk of the riders who stuck with the same team. The blue labels give the initials of the official name of each team, such as M-S (Mitchelton-Scott), MT (Movistar Team), T-S (Trek-Segafredo) and TS (Team Sunweb). Riders who switched teams are labelled in red.

Although there is a Dutch/German grouping on the lower right, the main structure is from the outside towards the centre of the network.

The spikes around the end of the chart show riders like Geoffrey Soupe or Rubén Fernández, who stepped down to smaller non World Tour teams like Team Total Direct Energie (TTDE), Nippo Delko One Provence (NNDP), Euskaltel-Euskadi (E-E), Androni Giocattoli-Sidermec (AG-S ) or U-XPCT (Uno-X Pro Cycling Team).

The two World Tour outliers were Mitchelton-Scott (M-S) and Groupama FDJ (GF), who retained virtually all their riders from 2019. Moving closer in, a group of teams lies around the edge of the central mass, where a few transfers occurred. Moving anti-clockwise we see CCC Team (CT), Astana Pro Team (APT), Trek-Segafredo (T-S), AG2R Le Mondial (ALM), Circus-Wanty Gobert (C-WG), Team Jumbo Visma (TJV), Bora-Hansgrohe (B-H) and EF Pro Cycling (EPC).

Deeper in the mêlée, Ineos (TI_19/IG_20), Deceuninck – Quick Step (D-QS), UAE-Team Emirates (U-TE), Lotto Soudal (LS), Bahrain – McLaren (B-H) and Movistar Team(MT) exchanged a number of riders.

Right in the centre Israel Start-Up Nation (IS-UN) grabbed a whole lot of riders, including 7 from Team Arkéa Samsic (TAS). Meanwhile likes of Victor Campenaerts and Domenico Pozzovivo are probably regretting joining NTT Pro Cycling (TDD_19/NPC_20).

Looking forward

A few of the top riders have contracts for next year showing up on ProCyclingStats. So far 2020/2021 looks like the network below. Many riders are renewing with their existing teams, indicated by the broad green lines. But some big names are changing teams, including Chris Froome, Richie Porte, Laurens De Plus, Sam Oomen, Romain Bardet and Wilco Keldeman, Bob Jungels and Lilian Calmejane.

What about networks of riders?

My original thought when starting this analysis was that over their careers, certain riders must have been team mates with most of the riders in today’s peloton, so who is the most connected? Unfortunately this turned out to be ridiculously complicated, as shown in the image below, where nodes are riders with links if they were ever teammates and the colours represent the current teams. The highest ranked rider in each team is shown in red.

It is hard to make much sense of this, other than to note that those with shorter careers in the same team are near the edge and that Philippe Gilbert is close to the centre. Out of interest, the rider around 9 o’clock linking Bora and Jumbo Visma is Christoph Pfingsten, who moved this year. At least we can conclude that professional cyclists are well-connected.

Lord of the (cycling) rings

Which Lord of the Rings characters do they look like? Ask an AI.

After building an app that uses deep learning to recognise Lord of the Rings characters, I had a bit of fun feeding in pictures of professional cyclists. This blog explains how the app works. If you just want to try it out yourself, you can find it here, but note that may need to be fairly patient, because it can take up to 5 minutes to fire up for the first time… it does start eventually.

Identifying wizards, hobbits and elves

The code that performs this task was based on the latest version of the excellent fast.ai course Practical Deep Learning for Coders. If you have done bit of programming in Python, you can build something like this yourself after just a few lessons.

The course sets out to defy some myths about deep learning. You don’t need to have a PhD in computer science – the fastai library is brilliantly designed and easy to use. Python is the language of choice for much of data science and the course runs in Jupyter notebooks.

You don’t need petabytes of data – I used fewer than 150 sample images of each character, downloaded using the Bing Image Search API. It is also straightforward to download publicly available neural networks within the fastai framework. These have been pre-trained to recognise a broad range of objects. Then it is relatively quick to fine-tune the parameters to achieve a specific task, such as recognising about 20 different Tolkien characters.

You don’t need expensive resources to build your models – I trained my neural network in just a few minutes, using a free GPU available on Google’s Colaboratory platform. After transferring the essential files to a github repository, I deployed the app at no cost, using Binder.

Thanks to the guidance provided by fastai, the whole process was quick and straightforward to do. In fact, by far the most time consuming task was cleaning up the data set of downloaded images. But there was a trick for doing this. First you train your network on whatever images come up in an initial search, until it achieves a reasonable degree of accuracy. Then take a look at the images that the model finds the most difficult to classify. I found that these tended to be pictures of lego figures or cartoon images. With the help of a fastai tool, it was simple to remove irrelevant images from the training and validation sets.

After a couple of iterations, I had a clean dataset and a great model, giving about 70% accuracy, which as good enough my purposes. Some examples are shown in the left column at the top of this blog.

The model’s performance was remarkably similar to my own. While Gollum is easy to identify, the wizard Saruman can be mistaken for Gandalf, Boromir looks a bit like Faramir and the hobbits Pippin and Merry can be confused.

Applications outside Middle Earth

One of the important limits of these types of image recognition models is that even if they work well in the domain in which they have been trained, they cannot be expected do a good job on totally different images. Nevertheless, I thought it would be amusing to supply the pictures of professional cyclists, particularly given the current vogue for growing facial hair.

My model was 87% sure that Peter Sagan was Boromir, but only 81.5% confident in the picture of Sean Bean. It was even more certain that Daniel Oss played the role of Faramir. Geraint Thomas was predicted to be Frodo Baggins, but with much lower confidence. I wondered for a while with Tadej Pogacar should be Legolas, but perhaps the model interpreted his outstretched arms as those of an archer.

I hoped that a heavily bearded Bradley Wiggins might come out as Gimli, but that did not not seem to work. Nevertheless it was entertaining to upload photographs of friends and family. With apologies for any waiting times to get to it running, you can try it here.

In earlier blogs, I have described similar models to identify common flowers or different types of bike.

Efficient COVID testing on a hypercube

A strategy for finding people infected with SARS-CoV-2: optimizing pooled testing at low prevalence, Mutesa et al

In previous blogs, I described how mathematical modelling can help understand the spread of the COVID-19 epidemics and provide privacy-preserving contact tracing. Looking forward at how the world will have to deal with COVID-19 in the coming months, it is likely that a significant percentage of the population will need to be tested multiple times. In a recent BBC science podcast, Neil Turok, Leon Mutesa and Wilfred Ndifo describe their highly efficient method of implementing large-scale testing that takes advantage of pooling samples. This is helping African governments save millions on the cost of testing. I offer an outline of their innovative approach, which is described in more detail in a paper published on arxiv.org.

The need for large-scale testing

The roll-out of antigen testing in some countries, like the US and the UK, has been painfully slow. Some suggest that the US may need to carry out between 400,00 and 900,000 tests a day in order to get a grip on the epidemic. When antigen tests cost 30-50 US dollars (or 24-40 UK pounds), this could be very expensive. However, as long as a relatively small percentage of the population is infected, running a separate test for everyone would be extremely inefficient compared with approaches that pool samples.

Pooling offers a huge advantage, because a negative test for a pooled sample of 100 swabs, would clear 100 people with a single test. The optimal size of the pools depends on the level of incidence of the disease: larger pools can be used for lower incidence.

The concept of pooling dates back to the work of Dorfman in 1943. His method was to choose an optimal pool size and perform a test on each pooled sample. A negative result for a pool clears all the samples contained in it. Then the infected individuals are found by testing every sample in the the positive pools. Mutesa and Ndifo’s hypercube method is more efficient, because, rather than testing everyone in an infected pool, you test carefully-selected sub-pools.

The idea is to imagine that all the samples in a pool lie on a multidimensional lattice in the form of a hypercube. It turns out that the optimal number of points in each direction is 3. Obviously it is hard to visualise high dimensions, but in 3-D, you have 27 samples arranged on a 3x3x3 grid forming a cube. The trick to identifying individual infected samples is to create sub-pools by taking slices through the lattice. In the diagram above, there are 3 red slices, 3 green and 3 blue, each containing 9 samples.

Consider, for simplicity, only one infected person out of the 27. Testing the 9 pools represented by the coloured slices will result in exactly 3 positive results, representing the intersection of the three planes passing through the infected sample. This uniquely identifies the positive individual with just 9 tests, whereas Dorfman would have set out to test all 27, finding the positive, on average after doing half of these.

Slicing a hypercube

Although you can optimise the pool size to ensure that the expected number of positives in any pool is manageable, in practice you won’t know how many infected samples are contained in any particular pool. The hypercube method deals with this by noting that a slice through a D-dimensional hypercube is itself a hypercube of dimension D-1, so the method can be applied recursively.

The other big advantage is that the approach is massively parallel, allowing positives to be identified quickly, relative to the speed of spread of the pandemic. About 3 rounds of PCR tests can be completed in a day. Algorithms that further reduce the total number of tests towards the information theoretical limit, such as binary search, require tests to be performed sequentially, which takes longer than doing more tests in parallel.

In order to make sure I really understood what is going on, I wrote some Python code to implement and validate the hypercube algorithm. In principle, it was extremely simple, but dealing with low probability edge cases, where multiple positive samples happen to fall into the same slice turned out to be a bit messy. However, in simulations, all infected samples were identified with no false positives nor false negatives. The number of tests was very much in line with the theoretical value.

Huge cost savings

My Python program estimates the cost savings of implementing the hypercube algorithm versus testing every sample individually. The bottom line is that the if the US government needed to test 900,000 people and the background level of infection is 1%, the algorithm would find all infected individuals with around 110,000 tests or 12% of the total samples. At $40 a test, this would be a cost saving of over $30million per day versus testing everyone individually. Equivalent calculations for the UK government to test 200,000 people would offer savings of around £5million pounds a day.

It is great to see leading edge science being developed in Africa. Cost conscious governments, for example in Rwanda, are implementing the strategy. Western governments lag behind, delayed by anecdotal comments from UK officials who worry that the approach is “too mathematical”, as if this is somehow a vice rather than a virtue.

References

A strategy for finding people infected with SARS-CoV-2:optimizing pooled testing at low prevalence, Mutesa et al

Privacy preserving COVID-19 tracking apps

As the initial global wave of COVID-19 infections is brought under control, the world is moving into a phase of extensive testing, tracking and tracing, until a vaccine can be found. The preservation of personal privacy must be paramount in these initiatives.

The UK government’s target of performing 100,000 tests a day by the end of April 2020 provided a fine example of Goodhart’s law: “When a measure becomes a target, it ceases to be a good measure”. One tragic consequence was the willingness, even encouragement, to define just about anything as a “completed test”, including the action of simply dispatching a kit by post. This has discouraged the distinguish between different types of test: antigen or antibody, nasal swab or blood test, pin-prick or venous sample, laboratory analysis or on-the-spot result.

For those who suspect they might have been exposed to COVID-19, an antibody test is the most useful. Although there has not been time to gather sufficient information to be absolutely sure, the detection of antibodies in the blood should provide immunity from infection, at least in the short term, unless the virus mutates sufficiently to bypass the immune response. Private tests are available from providers, such as Forth, where reliable results of IgG antibodies are provided by laboratory tests performed using the Abbot Architect method.

A second area where the UK government seems to be going wrong is in hiring thousands of people to carry out intrusive tracking and tracing. Not only is this hugely inefficient, it is also a massive unnecessary invasion of personal privacy. That a data leak occurred before it even started hardly inspires confidence.

Privacy Preserving Contact Tracing

A team of epidemiologist and cryptographers called DP-3T has released open source software that makes use of Bluetooth messages exchanged between mobile phones to track and trace COVID-19 infections entirely anonymously. It does not require users to surrender any personal information or location data. The approach is the basis for the technology announced jointly by Apple and Google.

The method is explained very nicely in this video 3Blue1Brown or in comic form by Nicky Case. This is a summary of how it works. Once you download a privacy preserving app onto your phone, it transmits random numbers over Bluetooth, at regular time intervals, and simultaneously listens for the random numbers of other users. Since the numbers are random, they contain no information about the you. Your phone locally maintains a list of your transmitted random numbers. It also stores locally a list of all numbers received, possibly including a timestamp and the Bluetooth signal strength, which gives some information about the proximity of the other user. Items older than, say, 14 days can be deleted from both lists.

If a person falls ill and tests positive for COVID-19 antigens, that person can voluntarily, with the permission of a healthcare professional, anonymously upload the list of transmitted random numbers to a central database. The phone app of every user periodically checks this database against its local list of received messages. If a match is detected, the app can identify the date, time and duration of contact, along with an estimate of proximity. This allows the app to advise a user to “self-isolate” for an appropriate period. This matching can all be done locally on the phone.

If set up appropriately, neither Google nor Apple nor any government body would be able to identify any particular individual. Privacy is preserved. No human trackers or tracers are required. No ankle bracelets or police guards are necessary. The system is entirely voluntary, but if sufficient users join up, say, 60% of those susceptible, it can still have a significant impact in controlling the spread of the virus. This is the correct way forward for a free and democratic society.